Files

camperbot 43a2a0a395 chore(i18n,learn): processed translations (#44866 )

2022-01-23 00:08:20 +09:00

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f49a1000cf542c50ffac	問題 300: タンパク質の折り畳み	5	301954	problem-300-protein-folding

--description--

非常に単純化すれば、タンパク質は疎水性要素 (H) と極性要素 (P) で構成される文字列と考えることができます。例えば、HHPPHHHPHHPH です。

この問題ではタンパク質の方向が重要であり、例えば HPP は PPH と区別されます。したがって、n 個の要素で構成される相異なるタンパク質は 2^n 種類存在します。

自然界では、これらの文字列は常に H-H 接点の数ができるだけ多くなるように折り畳まれています。その方がエネルギー面で有利だからです。

その結果、H 要素は内側に蓄積し、P 要素は外側に蓄積する傾向があります。

自然のタンパク質はもちろん三次元で折り畳まれていますが、ここでは二次元で折り畳まれるタンパク質のみを考えます。

下図は、上の例のタンパク質を折り畳む 2 通りの方法を示しています (赤い点は H-H 接点)。

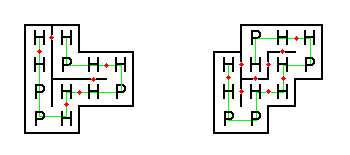
左側の折り畳みは H-H 接点が 6つしかないため、自然にこの形になることはあり得ないでしょう。一方、右側の折り畳みは H-H 接点が 9 つあり、この文字列には最適です。

文字列のいずれの位置にも H 要素と P 要素が同じ確率で存在すると仮定すると、長さ 8 の無作為なタンパク質文字列の最適な折り畳みにおいて、H-H 接点の平均数は \frac{850}{2^8} = 3.3203125 になります。

長さ 15 の無作為なタンパク質文字列の最適な折り畳みにおいて、H-H 接点の平均数はいくつですか。回答は、厳密な結果に対して適宜小数位を使用すること。

--hints--

proteinFolding() は 8.0540771484375 を返す必要があります。

assert.strictEqual(proteinFolding(), 8.0540771484375);

function proteinFolding() {

  return true;
}

proteinFolding();

// solution required