2.0 KiB
2.0 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4b71000cf542c50ffca | 問題 331: 十字めくり | 5 | 301989 | problem-331-cross-flips |
--description--
N×N 個の円盤が正方形のゲーム盤上に置かれています。 円盤にはそれぞれ黒い面と白い面があります。
ターンごとに円盤を 1 枚選び、それと同じ横列および同じ縦列にある円盤をすべて裏返します。したがって、2 × N - 1 枚の円盤が裏返されます。 すべての円盤が白い面になるとゲームは終了です。 次の例は、5×5 の盤を使用したゲームです。
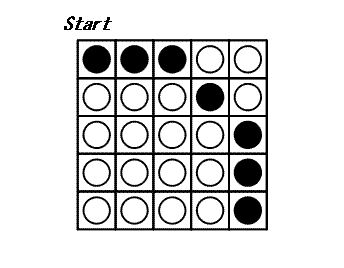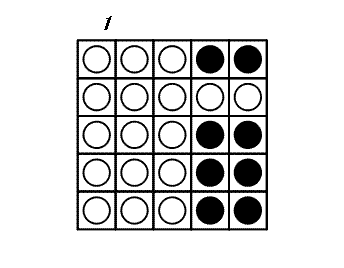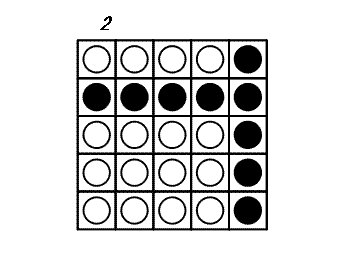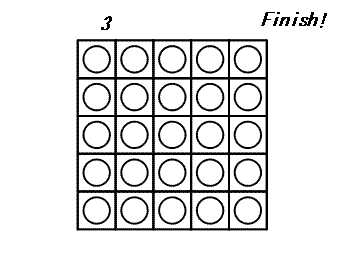
このゲームを終了するための最小ターン数が 3 であることが分かります。
N×N の盤の左下の円盤は座標 (0,0)、右下の円盤は座標 (N - 1,$0$)、そして左上の円盤は座標 (0,$N - 1$) です。
N × N 枚の円盤を並べた盤について、N - 1 \le \sqrt{x^2 + y^2} \lt N を満たす (x, y) の円盤は黒い面が見え、それ以外は白い面が見えているような配置を、C_N とします。 上図は C_5 です。
配置 C_N からゲームを始めて終了するまでの最小ターン数を T(N) とし、配置 C_N に解が存在しない場合は最小ターン数を 0 とします。 T(5) = 3 であることは既に示しました。 さらに、T(10) = 29 と T(1\\000) = 395\\,253 が与えられます。
\displaystyle \sum_{i = 3}^{31} T(2^i - i) を求めなさい。
--hints--
crossFlips() は 467178235146843500 を返す必要があります。
assert.strictEqual(crossFlips(), 467178235146843500);
--seed--
--seed-contents--
function crossFlips() {
return true;
}
crossFlips();
--solutions--
// solution required