1.5 KiB
1.5 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5001000cf542c510012 | 問題 404: 交差楕円 | 5 | 302072 | problem-404-crisscross-ellipses |
--description--
E_a は 式 x^2 + 4y^2 = 4a^2 で表される楕円です。
E_a' は、原点 O(0, 0) を中心に、0° < θ < 90° の範囲内で、E_a を反時計回りに θ 度回転させた像です。
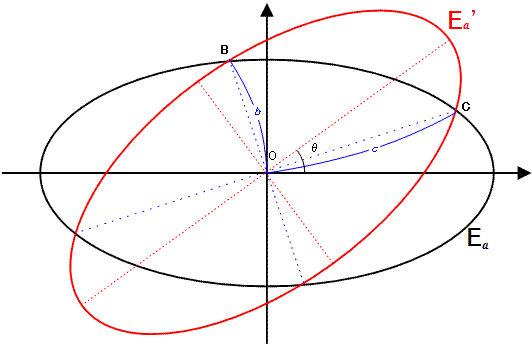
原点に最も近い 2 つの交点から原点までの距離を $b$、それ以外の 2 つの交点から原点までの距離を c とします。
a, b, c が正の整数の場合、順序付き三つ組数 (a, b, c) を正準楕円三つ組数と呼びます。
例えば、(209、247、286) は正準楕円三つ組数です。
a ≤ N に対し、相異なる正準楕円三つ組数 (a, b, c) の個数を C(N) とします。
C({10}^3) = 7, C({10}^4) = 106, C({10}^6) = 11\\,845 であることを確認できます。
C({10}^{17}) を求めなさい。
--hints--
crisscrossEllipses() は 1199215615081353 を返す必要があります。
assert.strictEqual(crisscrossEllipses(), 1199215615081353);
--seed--
--seed-contents--
function crisscrossEllipses() {
return true;
}
crisscrossEllipses();
--solutions--
// solution required