Files

camperbot 43a2a0a395 chore(i18n,learn): processed translations (#44866 )

2022-01-23 00:08:20 +09:00

1.9 KiB

Raw Permalink Blame History

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f5131000cf542c510025	問題 422: 双曲線上の点列	5	302092	problem-422-sequence-of-points-on-a-hyperbola

--description--

式 12x^2 + 7xy - 12y^2 = 625 で定義される双曲線を H とします。

次に、点 (7, 1) を X と定義します。 X が H 上にあることが分かります。

ここで、H, \\{P_i : i ≥ 1\\} の点列を次のように定義します。

P_1 = (13, \frac{61}{4})
P_2 = (\frac{-43}{6}, -4)
i > 2 のとき、P_i は、線 P_iP_{i - 1} が線 P_{i - 2}X と平行になるような点のうち P_{i - 1} ではない方の、H 上の一意の点である。 P_i を明確に定義できること、および、それらの座標が常に有理数であることを示せる。

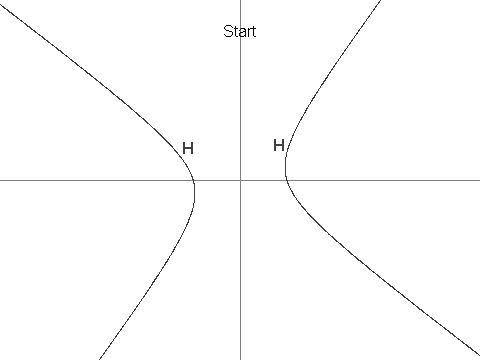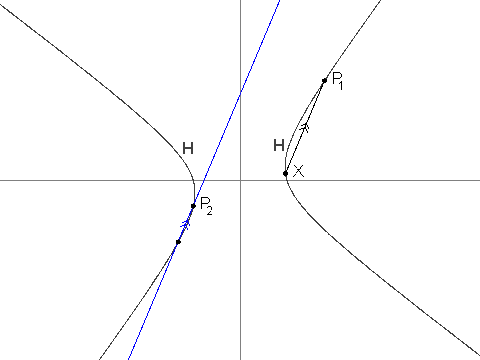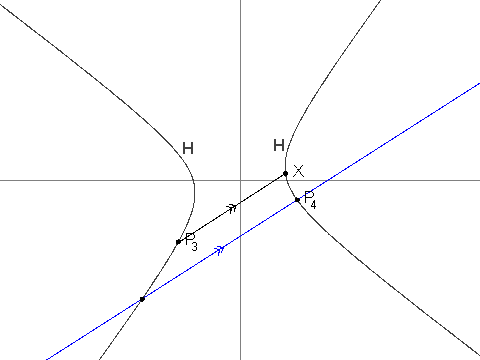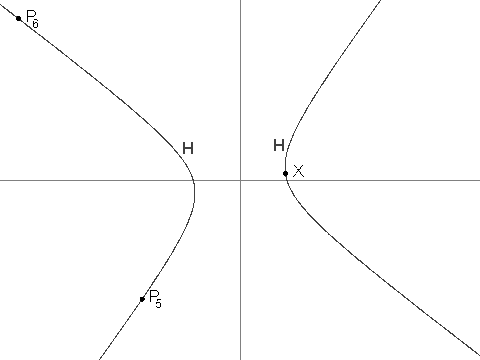
P_3 = (\frac{-19}{2}, \frac{-229}{24}), P_4 = (\frac{1267}{144}, \frac{-37}{12}), P_7 = (\frac{17\\,194\\,218\\,091}{143\\,327\\,232}, \frac{274\\,748\\,766\\,781}{1\\,719\\,926\\,784}) が与えられます。

n = {11}^{14} のとき、P_n を次の形式で求めなさい: P_n = (\frac{a}{b}, \frac{c}{d}) が既約分数かつ分母が正の数である場合、回答は (a + b + c + d)\bmod 1\\,000\\,000\\,007 となります。

n = 7 のとき、回答は 806\\,236\\,837 です。

--hints--

sequenceOfPointsOnHyperbola() は 92060460 を返す必要があります。

assert.strictEqual(sequenceOfPointsOnHyperbola(), 92060460);

--seed--

--seed-contents--

function sequenceOfPointsOnHyperbola() {

  return true;
}

sequenceOfPointsOnHyperbola();

--solutions--

// solution required

1.9 KiB Raw Permalink Blame History