Files

camperbot 43a2a0a395 chore(i18n,learn): processed translations (#44866 )

2022-01-23 00:08:20 +09:00

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f5431000cf542c510056	問題 471: 楕円に内接する三角形	5	302148	problem-471-triangle-inscribed-in-ellipse

--description--

0 < 2b < a を満たす整数 a, b について、三角形 ΔABC は式 \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 で表される楕円に内接しています。

三角形 ΔABC の内接円の中心が (2b, 0) で、A の座標が \left(\frac{a}{2}, \frac{\sqrt{3}}{2}b\right) のとき、その内接円の半径を r(a, b) とします。

たとえば、r(3, 1) = \frac{1}{2}, r(6, 2) = 1, r(12, 3) = 2 です。

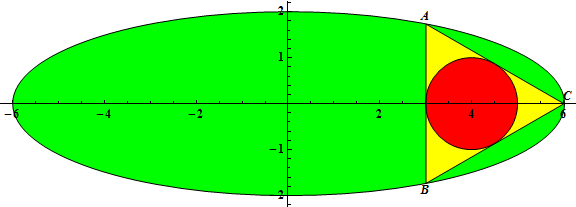
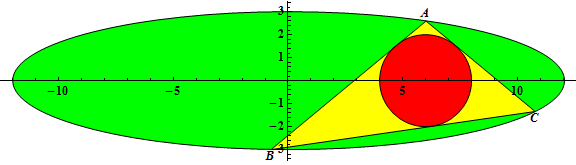
G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b) と定義します。

G(10) = 20.59722222, G(100) = 19223.60980 (有効数字 10 桁に四捨五入) が与えられます。

G({10}^{11}) を求めなさい。回答は、有効数字 10 桁に四捨五入された科学的記数法の文字列にすること。また、小文字 e で仮数部と指数部を区切ること。

G(10) の場合、回答は 2.059722222e1 となります。

--hints--

triangleInscribedInEllipse() は文字列を返す必要があります。

assert(typeof triangleInscribedInEllipse() === 'string');

triangleInscribedInEllipse() は文字列 1.895093981e31 を返す必要があります。

assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');

function triangleInscribedInEllipse() {

  return true;
}

triangleInscribedInEllipse();

// solution required