freeCodeCamp/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-143-investigating-the-torricelli-point-of-a-triangle.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f3fc1000cf542c50ff0e	問題 143：三角形托裏拆利點的研究	5	301772	problem-143-investigating-the-torricelli-point-of-a-triangle

--description--

設三角形 ABC 的內角均小於120度。 取三角形內任意一點 X，令 $XA = p$，$XC = q$，$XB = r$。

費馬曾經向托裏拆利提出挑戰：找到令 p + q + r 最小的點 X 的位置。

托裏拆利證明，若對三角形 ABC 三邊分別構造等邊三角形 AOB、BNC 和 AMC，則三角形 AOB、BNC 和 AMC 的外接圓相交於三角形 ABC 內的一點 T。 此外，他還證明這個後來被稱爲托裏拆利點或費馬點的點 T，就是使得 p + q + r 最小的點。 更值得注意的是，當和最小時，滿足 AN = BM = CO = p + q + r 且 AN、BM 和 CO 也相交於點 T。

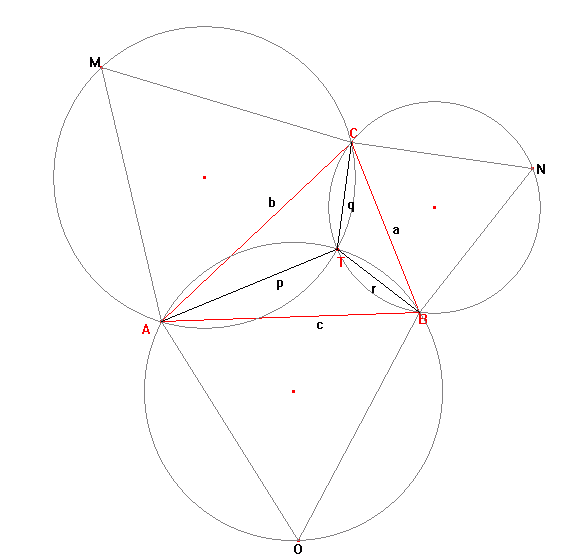
如果當和最小時且有 a、b、c、p、q 和 r 均爲正整數，我們就稱三角形 ABC 爲托裏拆利三角形。 例如，$a = 399$、$b = 455$、c = 511 就是一個托裏拆利三角形，此時 $p + q + r = 784$。 對於所有滿足 p + q + r ≤ 120000 的托裏拆利三角形，求出所有不同值的總和。

--hints--

sumTorricelliTriangles() 應該返回 30758397。

assert.strictEqual(sumTorricelliTriangles(), 30758397);

--seed--

--seed-contents--

function sumTorricelliTriangles() {

  return true;
}

sumTorricelliTriangles();

--solutions--

// solution required