* fix: clean-up Project Euler 121-140 * fix: corrections from review Co-authored-by: Sem Bauke <46919888+Sembauke@users.noreply.github.com> * fix: missing backticks Co-authored-by: Kristofer Koishigawa <scissorsneedfoodtoo@gmail.com> * fix: corrections from review Co-authored-by: Tom <20648924+moT01@users.noreply.github.com> * fix: missing delimiter Co-authored-by: Sem Bauke <46919888+Sembauke@users.noreply.github.com> Co-authored-by: Kristofer Koishigawa <scissorsneedfoodtoo@gmail.com> Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
1.4 KiB
1.4 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f3f71000cf542c50ff0a | Problem 139: Pythagorean tiles | 5 | 301767 | problem-139-pythagorean-tiles |
--description--
Let (a, b, c) represent the three sides of a right angle triangle with integral length sides. It is possible to place four such triangles together to form a square with length c.
For example, (3, 4, 5) triangles can be placed together to form a 5 by 5 square with a 1 by 1 hole in the middle and it can be seen that the 5 by 5 square can be tiled with twenty-five 1 by 1 squares.
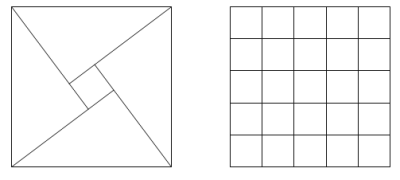
However, if (5, 12, 13) triangles were used, the hole would measure 7 by 7. These 7 by 7 squares could not be used to tile the 13 by 13 square.
Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to occur?
--hints--
pythagoreanTiles() should return 10057761.
assert.strictEqual(pythagoreanTiles(), 10057761);
--seed--
--seed-contents--
function pythagoreanTiles() {
return true;
}
pythagoreanTiles();
--solutions--
// solution required