* fix: clean-up Project Euler 281-300 * fix: missing image extension * fix: missing power Co-authored-by: Tom <20648924+moT01@users.noreply.github.com> * fix: missing subscript Co-authored-by: Tom <20648924+moT01@users.noreply.github.com> Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
1.7 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4931000cf542c50ffa6 | Problem 295: Lenticular holes | 5 | 301947 | problem-295-lenticular-holes |
--description--
We call the convex area enclosed by two circles a lenticular hole if:
- The centres of both circles are on lattice points.
- The two circles intersect at two distinct lattice points.
- The interior of the convex area enclosed by both circles does not contain any lattice points.
Consider the circles:
$$\begin{align} & C_0: x^2 + y^2 = 25 \\ & C_1: {(x + 4)}^2 + {(y - 4)}^2 = 1 \\ & C_2: {(x - 12)}^2 + {(y - 4)}^2 = 65 \end{align}$$
The circles C_0, C_1 and C_2 are drawn in the picture below.
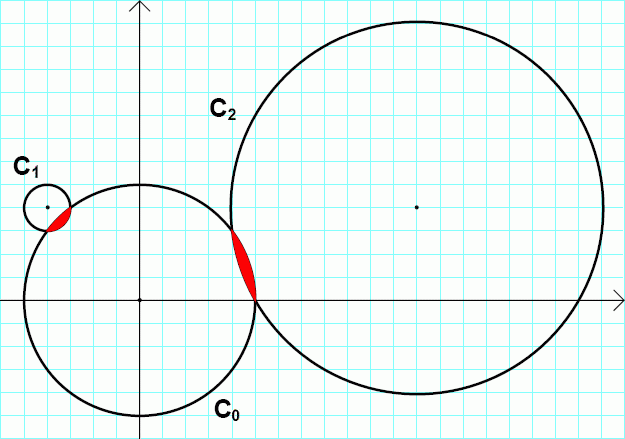
C_0 and C_1 form a lenticular hole, as well as C_0 and C_2.
We call an ordered pair of positive real numbers (r_1, r_2) a lenticular pair if there exist two circles with radii r_1 and r_2 that form a lenticular hole. We can verify that (1, 5) and (5, \sqrt{65}) are the lenticular pairs of the example above.
Let L(N) be the number of distinct lenticular pairs (r_1, r_2) for which 0 < r_1 ≤ r_2 ≤ N. We can verify that L(10) = 30 and L(100) = 3442.
Find L(100\\,000).
--hints--
lenticularHoles() should return 4884650818.
assert.strictEqual(lenticularHoles(), 4884650818);
--seed--
--seed-contents--
function lenticularHoles() {
return true;
}
lenticularHoles();
--solutions--
// solution required