freeCodeCamp/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f4b91000cf542c50ffcb	Problem 332: Spherical triangles	5	301990	problem-332-spherical-triangles

--description--

A spherical triangle is a figure formed on the surface of a sphere by three great circular arcs intersecting pairwise in three vertices.

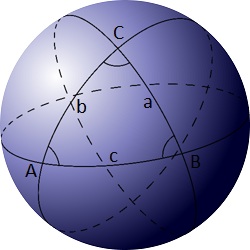
Let C(r) be the sphere with the centre (0,0,0) and radius r.

Let Z(r) be the set of points on the surface of C(r) with integer coordinates.

Let T(r) be the set of spherical triangles with vertices in Z(r). Degenerate spherical triangles, formed by three points on the same great arc, are not included in T(r).

Let A(r) be the area of the smallest spherical triangle in T(r).

For example A(14) is 3.294040 rounded to six decimal places.

Find \displaystyle \sum_{r = 1}^{50} A(r). Give your answer rounded to six decimal places.

--hints--

sphericalTriangles() should return 2717.751525.

assert.strictEqual(sphericalTriangles(), 2717.751525);

--seed--

--seed-contents--

function sphericalTriangles() {

  return true;
}

sphericalTriangles();

--solutions--

// solution required