* fix: clean-up Project Euler 361-380 * fix: improve wording Co-authored-by: Sem Bauke <46919888+Sembauke@users.noreply.github.com> * fix: remove unnecessary paragraph * fix: corrections from review Co-authored-by: Tom <20648924+moT01@users.noreply.github.com> Co-authored-by: Sem Bauke <46919888+Sembauke@users.noreply.github.com> Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
2.1 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4d91000cf542c50ffeb | Problem 363: Bézier Curves | 5 | 302024 | problem-363-bzier-curves |
--description--
A cubic Bézier curve is defined by four points: P_0, P_1, P_2 and P_3.
The curve is constructed as follows:
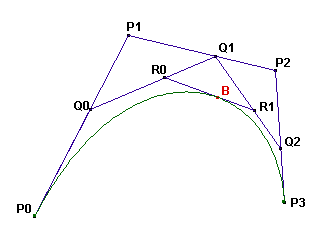
On the segments P_0P_1, P_1P_2 and P_2P_3 the points Q_0,$Q_1$ and Q_2 are drawn such that \frac{P_0Q_0}{P_0P_1} = \frac{P_1Q_1}{P_1P_2} = \frac{P_2Q_2}{P_2P_3} = t, with t in [0,1].
On the segments Q_0Q_1 and Q_1Q_2 the points R_0 and R_1 are drawn such that \frac{Q_0R_0}{Q_0Q_1} = \frac{Q_1R_1}{Q_1Q_2} = t for the same value of t.
On the segment R_0R_1 the point B is drawn such that \frac{R_0B}{R_0R_1} = t for the same value of t.
The Bézier curve defined by the points P_0, P_1, P_2, P_3 is the locus of B as Q_0 takes all possible positions on the segment P_0P_1. (Please note that for all points the value of t is the same.)
From the construction it is clear that the Bézier curve will be tangent to the segments P_0P_1 in P_0 and P_2P_3 in P_3.
A cubic Bézier curve with P_0 = (1, 0), P_1 = (1, v), P_2 = (v, 1) and P_3 = (0, 1) is used to approximate a quarter circle. The value v > 0 is chosen such that the area enclosed by the lines OP_0, OP_3 and the curve is equal to \frac{π}{4} (the area of the quarter circle).
By how many percent does the length of the curve differ from the length of the quarter circle? That is, if L is the length of the curve, calculate 100 × \displaystyle\frac{L − \frac{π}{2}}{\frac{π}{2}}. Give your answer rounded to 10 digits behind the decimal point.
--hints--
bezierCurves() should return 0.0000372091.
assert.strictEqual(bezierCurves(), 0.0000372091);
--seed--
--seed-contents--
function bezierCurves() {
return true;
}
bezierCurves();
--solutions--
// solution required