1.4 KiB
1.4 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5001000cf542c510012 | Problem 404: Crisscross Ellipses | 5 | 302072 | problem-404-crisscross-ellipses |
--description--
E_a is an ellipse with an equation of the form x^2 + 4y^2 = 4a^2.
E_a' is the rotated image of E_a by θ degrees counterclockwise around the origin O(0, 0) for 0° < θ < 90°.
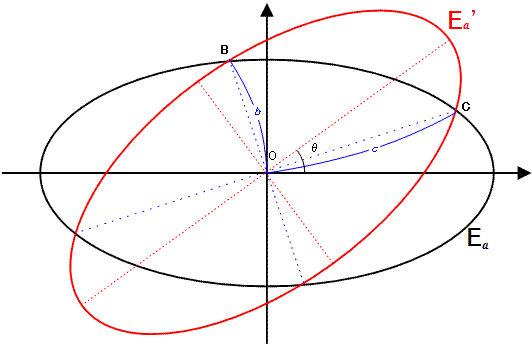
b is the distance to the origin of the two intersection points closest to the origin and c is the distance of the two other intersection points.
We call an ordered triplet (a, b, c) a canonical ellipsoidal triplet if a, b and c are positive integers.
For example, (209, 247, 286) is a canonical ellipsoidal triplet.
Let C(N) be the number of distinct canonical ellipsoidal triplets (a, b, c) for a ≤ N.
It can be verified that C({10}^3) = 7, C({10}^4) = 106 and C({10}^6) = 11\\,845.
Find C({10}^{17}).
--hints--
crisscrossEllipses() should return 1199215615081353.
assert.strictEqual(crisscrossEllipses(), 1199215615081353);
--seed--
--seed-contents--
function crisscrossEllipses() {
return true;
}
crisscrossEllipses();
--solutions--
// solution required