1.7 KiB
1.7 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5191000cf542c51002b | Problem 428: Necklace of Circles | 5 | 302098 | problem-428-necklace-of-circles |
--description--
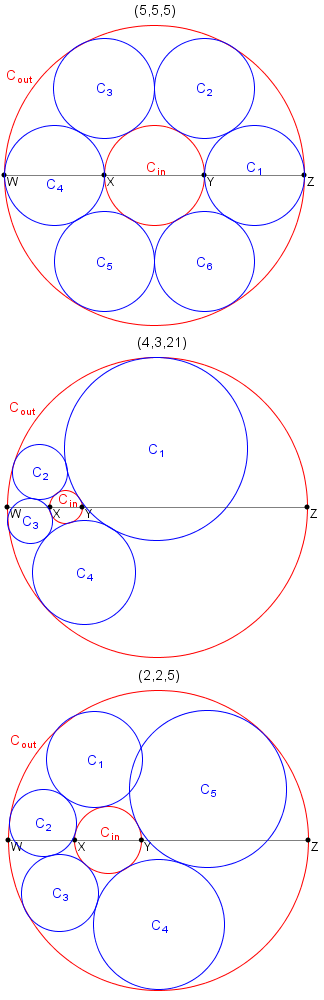
Let a, b and c be positive numbers.
Let W, X, Y, Z be four collinear points where |WX| = a, |XY| = b, |YZ| = c and |WZ| = a + b + c.
Let C_{\text{in}} be the circle having the diameter XY.
Let C_{\text{out}} be the circle having the diameter WZ.
The triplet (a, b, c) is called a necklace triplet if you can place k ≥ 3 distinct circles C_1, C_2, \ldots, C_k such that:
C_ihas no common interior points with anyC_jfor1 ≤ i,j ≤ kandi ≠ j,C_iis tangent to bothC_{\text{in}}andC_{\text{out}}for1 ≤ i ≤ k,C_iis tangent toC_{i + 1}for1 ≤ i < k, andC_kis tangent toC_1.
For example, (5, 5, 5) and (4, 3, 21) are necklace triplets, while it can be shown that (2, 2, 5) is not.
Let T(n) be the number of necklace triplets (a, b, c) such that a, b and c are positive integers, and b ≤ n. For example, T(1) = 9, T(20) = 732 and T(3\\,000) = 438\\,106.
Find T(1\\,000\\,000\\,000).
--hints--
necklace(1000000000) should return 747215561862.
assert.strictEqual(necklace(1000000000), 747215561862);
--seed--
--seed-contents--
function necklace(n) {
return true;
}
necklace(1000000000)
--solutions--
// solution required