freeCodeCamp/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f5431000cf542c510056	Problem 471: Triangle inscribed in ellipse	5	302148	problem-471-triangle-inscribed-in-ellipse

--description--

The triangle ΔABC is inscribed in an ellipse with equation \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, 0 < 2b < a, a and b integers.

Let r(a, b) be the radius of the incircle of ΔABC when the incircle has center (2b, 0) and A has coordinates \left(\frac{a}{2}, \frac{\sqrt{3}}{2}b\right).

For example, r(3, 1) = \frac{1}{2}, r(6, 2) = 1, r(12, 3) = 2.

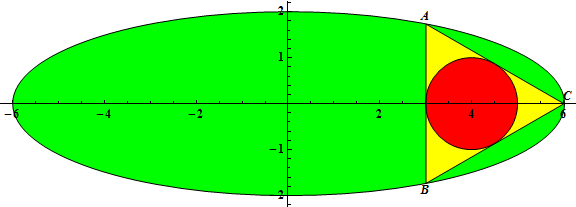
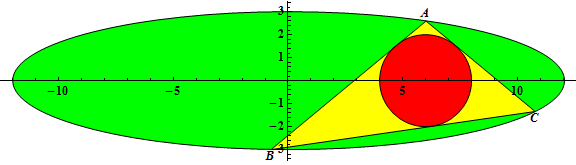
Let G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)

You are given G(10) = 20.59722222, G(100) = 19223.60980 (rounded to 10 significant digits).

Find G({10}^{11}). Give your answer as a string in scientific notation rounded to 10 significant digits. Use a lowercase e to separate mantissa and exponent.

For G(10) the answer would have been 2.059722222e1

--hints--

triangleInscribedInEllipse() should return a string.

assert(typeof triangleInscribedInEllipse() === 'string');

triangleInscribedInEllipse() should return the string 1.895093981e31.

assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');

--seed--

--seed-contents--

function triangleInscribedInEllipse() {

  return true;
}

triangleInscribedInEllipse();

--solutions--

// solution required