1.8 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f3ec1000cf542c50feff | Problema 128: differenze di mattonelle esagonali | 5 | 301755 | problem-128-hexagonal-tile-differences |
--description--
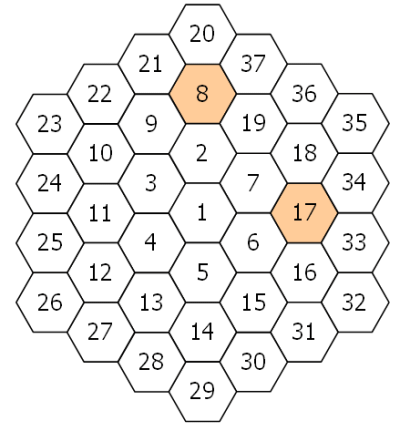
Una mattonella esagonale con il numero 1 è circondata da un anello di sei mattonelle esagonali, partendo dalla posizione delle dodici in punto numerate da 2 a 7 in direzione antioraria.
Nuovi anelli sono aggiungi nello stesso modo, con i nuovi anelli numerati da 8 a 19, da 20 a 37, da 38 a 61, e così via. Il diagramma qua sotto mostra i primi tre anelli.
Trovando la differenza tra la mattonella n e ognuna delle sei mattonelle vicine, definiamo PD(n) come il numero delle differenze che sono numeri primi.
Per esempio, lavorando in senso orario attorno alla mattonella 8 le differenze sono 12, 29, 11, 6, 1, e 13. Quindi PD(8) = 3.
Allo stesso modo le differenze attorno alla mattonella 17 sono 1, 17, 16, 1, 11, e 10, quindi PD(17) = 2.
SI può dimostrare che il valore massimo di PD(n) è 3.
Se tutte le mattonelle per cui PD(n) = 3 sono elencate in ordine crescente a formare una sequenza, la decima mattonella sarebbe 271.
Trova la 2000-sima mattonella nella sequenza.
--hints--
hexagonalTile() dovrebbe restituire 14516824220.
assert.strictEqual(hexagonalTile(), 14516824220);
--seed--
--seed-contents--
function hexagonalTile() {
return true;
}
hexagonalTile();
--solutions--
// solution required