freeCodeCamp/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-143-investigating-the-torricelli-point-of-a-triangle.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f3fc1000cf542c50ff0e	Problema 143: Investigare il punto Torricelli di un triangolo	5	301772	problem-143-investigating-the-torricelli-point-of-a-triangle

--description--

Sia ABC un triangolo con tutti gli angoli interni inferiori a 120 gradi. Sia X qualsiasi punto dentro il triangolo e siano XA = p, XC = q, w XB = r.

Fermat sfidò Torricelli a trovare la posizione di X per cui p + q + r è minimizzata.

Torricelli fu in grado di provare che se i triangoli equilateri AOB, BNC e AMC sono costruiti su ogni lato del triangolo ABC, i cerchi circoscritti AOB, BNC, e AMC intersecano in un singolo punto, T, dentro il triangolo. In più ha provato che T, chiamato il punto Torricelli/Fermat, minimizza p + q + r. Ancora più notevole, si può mostrare che quando la somma è minimizzata, AN = BM = CM = p + q + r e quindi AN, BM e CO pure intersecano in T.

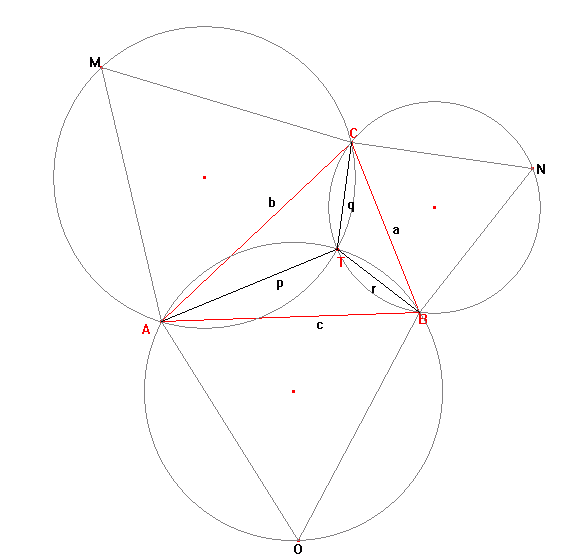
Se la somma è minimizzata e a, b, c, p, q e r sono tutti numeri interi positivi, chiamiamo il triangolo ABC un triangolo di Torricelli. Per esempio, a = 399, b = 455, c = 511 è un esempio di un Triangolo di Torricelli, con p + q + r = 784. Trova la somma di tutti i distinti valori di p + q + r ≤ 120000 per i triangoli di Torricelli.

--hints--

sumTorricelliTriangles() dovrebbe restituire 30758397.

assert.strictEqual(sumTorricelliTriangles(), 30758397);

--seed--

--seed-contents--

function sumTorricelliTriangles() {

  return true;
}

sumTorricelliTriangles();

--solutions--

// solution required