1.6 KiB
1.6 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f41a1000cf542c50ff2d | Problema 174: Contare il numero di lamine quadrate "cave" che possono formare uno, due, tre, ... disposizioni distinte | 5 | 301809 | problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-----distinct-arrangements |
--description--
Definiremo una lamina quadrata come un contorno quadrato con un "foro" quadrato in modo che la forma possieda simmetria verticale e orizzontale.
Date otto piastrelle è possibile formare una lamina in un solo modo: quadrato 3x3 con un foro 1x1 nel mezzo. Tuttavia, utilizzando trentadue piastrelle è possibile formare due lamine distinte.
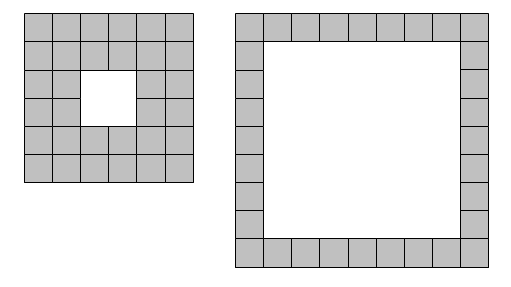
Se t rappresenta il numero di piastrelle utilizzate, diremo che t = 8 è di tipo L(1) e t = 32 è di tipo L(2).
Lascia che N(n) sia il numero di t ≤ 1000000 in modo che t sia di tipo L(n); per esempio, N(15) = 832.
Qual è \sum N(n) per 1 ≤ n ≤ 10?
--hints--
hollowSquareLaminaeDistinctArrangements() dovrebbe restituire 209566.
assert.strictEqual(hollowSquareLaminaeDistinctArrangements(), 209566);
--seed--
--seed-contents--
function hollowSquareLaminaeDistinctArrangements() {
return true;
}
hollowSquareLaminaeDistinctArrangements();
--solutions--
// solution required