freeCodeCamp/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-275-balanced-sculptures.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f4801000cf542c50ff92	Problema 275: Sculture Bilanciate	5	301925	problem-275-balanced-sculptures

--description--

Definiamo una scultura bilanciata di ordine n come segue:

• Un poliomino fatto di n + 1 mattonelle noti come i blocchi (n mattonelle) e il plinto (la mattonella rimanente);
• il plinto ha il suo centro in posizione (x = 0, y = 0);
• i blocchi hanno coordinate y maggiori di zero (quindi il plinto è l'unica piastrella più in basso);
• il centro di massa di tutti i blocchi, combinati, ha una coordinata di x pari a zero.

Quando si contano le strutture, qualsiasi arrangiamento che è una semplice riflessione lungo l'asse y, non viene contato come distinto. Per esempio, le 18 sculture bilanciate di ordine 6 sono mostrate di seguito; nota che ogni coppia d'immagini specchiate (intorno all'asse y) è contata come una sola scultura:

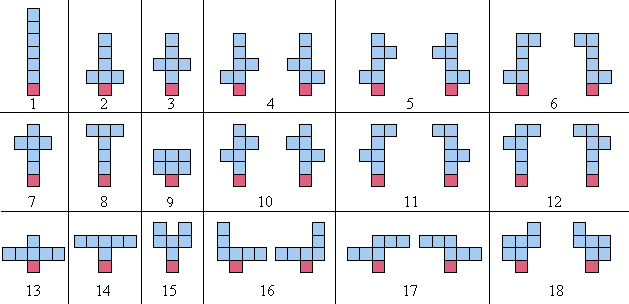
Ci sono 964 sculture bilanciate di ordine 10 e 360505 di ordine 15.

Quante sculture bilanciate di ordine 18 ci sono?

--hints--

balancedSculptures() dovrebbe restituire 15030564.

assert.strictEqual(balancedSculptures(), 15030564);

--seed--

--seed-contents--

function balancedSculptures() {

  return true;
}

balancedSculptures();

--solutions--

// solution required