2.0 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4c51000cf542c50ffd7 | Problema 344: Gioco del dollaro d'argento | 5 | 302003 | problem-344-silver-dollar-game |
--description--
Una variante del gioco del dollaro d'argento di N.G. de Brujin può essere descritta come segue:
Su una striscia di quadrati viene messo un certo numero di monete, al massimo una moneta per quadrato. Solo una moneta, chiamata dollaro d'argento, ha un valore. Due giocatori fanno mosse a turno. Ad ogni turno un giocatore deve fare una mossa regolare o speciale.
Una mossa regolare consiste nel selezionare una moneta e spostarla uno o più quadrati a sinistra. La moneta non può uscire dalla striscia o saltare sopra o al di là di un'altra moneta.
In alternativa, il giocatore può scegliere di fare la mossa speciale di intascare la moneta più a sinistra invece che fare una mossa regolare. Se non sono possibili mosse regolari, il giocatore è costretto a intascare la moneta più a sinistra.
Il vincitore è il giocatore che intasca il dollaro d'argento.
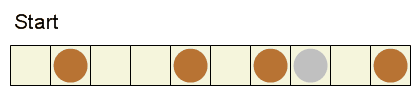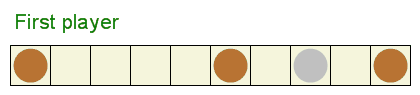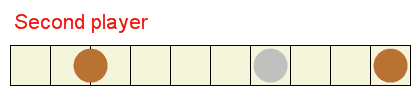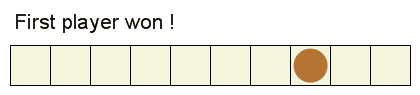
Una configurazione vincente è una disposizione di monete sulla striscia dove il primo giocatore può forzare una vittoria indipendentemente da cosa fa il secondo giocatore.
Sia W(n, c) il numero di configurazioni vincenti per una striscia di n quadrati, c monete senza valore e un dollaro d'argento.
Ti viene dato che W(10, 2) = 324 and W(100, 10) = 1\\,514\\,704\\,946\\,113\\,500.
Trova W(1\\,000\\,000, 100) modulo il semiprimo 1000\\,036\\,000\\,099 (= 1\\,000\\,003 \times 1\\,000\\,033).
--hints--
silverDollarGame() dovrebbe restituire 65579304332.
assert.strictEqual(silverDollarGame(), 65579304332);
--seed--
--seed-contents--
function silverDollarGame() {
return true;
}
silverDollarGame();
--solutions--
// solution required