freeCodeCamp/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-68-magic-5-gon-ring.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f3b01000cf542c50fec3	Problema 68: Anello pentagonale magico	5	302180	problem-68-magic-5-gon-ring

--description--

Considera il seguente anello trigonale, riempito con i numeri da 1 a 6, e con ogni riga che somma a nove.

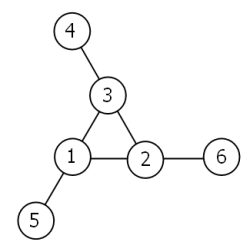
Lavorando in senso orario e iniziando dal gruppo di tre con il nodo esterno numericamente più piccolo (4, 3, 2 in questo esempio), ogni soluzione può essere descritta in modo univoco. Per esempio, la soluzione sopra può essere descritta dal set: 4,3,2; 6,2,1; 5,1,3.

È possibile completare l'anello con quattro somme diverse: 9, 10, 11, e 12. Ci sono otto soluzioni in totale.

!!crwdBlockTags_6_sgaTkcolBdwrc!!	!!crwdBlockTags_7_sgaTkcolBdwrc!!
9	4,2,3; 5,3,1; 6,1,2
9	4,3,2; 6,2,1; 5,1,3
10	2,3,5; 4,5,1; 6,1,3
10	2,5,3; 6,3,1; 4,1,5
11	1,4,6; 3,6,2; 5,2,4
11	1,6,4; 5,4,2; 3,2,6
12	1,5,6; 2,6,4; 3,4,5
12	1,6,5; 3,5,4; 2,4,6

Concatenando ogni gruppo è possibile formare stringhe a 9 cifre; la stringa più grande per un anello trigonale è 432621513.

Usando i numeri da 1 a 10, a seconda dell'arrangiamento, è possibile formare stringhe a 16 e 17 cifre. Qual è la stringa più grande a 16 cifre per un anello pentagonale "magico"?

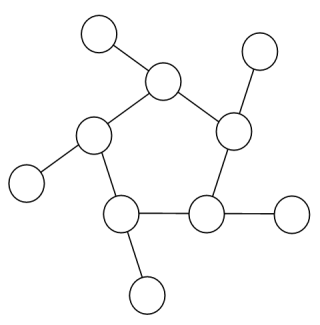
--hints--

magic5GonRing() dovrebbe restituire un numero.

assert(typeof magic5GonRing() === 'number');

magic5GonRing() dovrebbe restituire 6531031914842725.

assert.strictEqual(magic5GonRing(), 6531031914842725);

--seed--

--seed-contents--

function magic5GonRing() {

  return true;
}

magic5GonRing();

--solutions--

// solution required