1.5 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f3ea1000cf542c50fefd | Problema 126: Camadas de cuboides | 5 | 301753 | problem-126-cuboid-layers |
--description--
A número mínimo de cubos para cobrir todas as faces visíveis de um cuboide medindo 3 x 2 x 1 é 22.
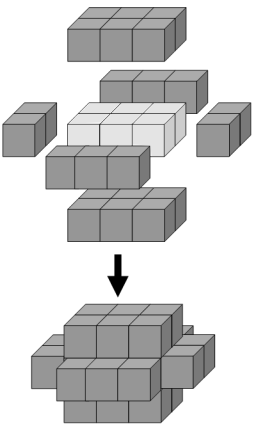
Se adicionarmos uma segunda camada a este sólido, precisaremos de 46 cubos para cobrir todas as faces visíveis, a terceira camada precisará de 78 cubos e a quarta camada precisará de 118 cubos para cobrir todas as faces visíveis.
No entanto, a primeira camada de um cuboide que mede 5 x 1 x 1 também precisa de 22 cubos; analogamente, a primeira camada de cuboides que medem 5 x 3 x 1, 7 x 2 x 1 e 11 x 1 x 1 contém 46 cubos.
Definiremos C(n) como a representação do número de cubos que contêm n cubos em uma de suas camadas. Portanto, C(22) = 2, C(46) = 4, C(78) = 5 e C(118) = 8.
Acontece que 154 é o menor valor de n no qual C(n) = 10.
Calcule o menor valor de n no qual C(n) = 1000.
--hints--
cuboidLayers() deve retornar 18522.
assert.strictEqual(cuboidLayers(), 18522);
--seed--
--seed-contents--
function cuboidLayers() {
return true;
}
cuboidLayers();
--solutions--
// solution required