1.8 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f40f1000cf542c50ff22 | Problema 163: Triângulos cruzados | 5 | 301797 | problem-163-cross-hatched-triangles |
--description--
Considere um triângulo equilátero em que linhas retas são desenhadas a partir de cada vértice até o meio do lado oposto, como no triângulo de tamanho 1 no esboço abaixo.
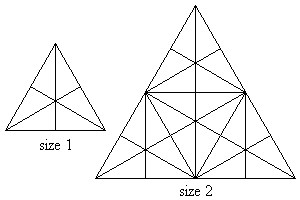
Agora, nesse triângulo, podem ser observados dezesseis triângulos de forma, tamanho, orientação ou localização diferentes. Usando o triângulos de tamanho 1 como blocos de construção, triângulos maiores podem ser formados, como o de tamanho 2 no esboço acima. Agora, nesse triângulo de lado 2, podem ser observados 104 triângulos de forma, tamanho, orientação ou localização diferentes.
É possível observar que o triângulo de tamanho 2 contém como blocos de construção 4 triângulos de tamanho 1. Um triângulo de tamanho 3 contém 9 blocos de construção de triângulos de tamanho 1, e um triângulo de tamanho n teria, portanto, n^2 blocos de construção de triângulos de tamanho 1.
Se quisermos indicar que T(n) é o número de triângulos presentes em um triângulo de tamanho n, então
$$\begin{align} & T(1) = 16 \\ & T(2) = 104 \end{align}$$
Encontre T(36).
--hints--
crossHatchedTriangles() deve retornar 343047.
assert.strictEqual(crossHatchedTriangles(), 343047);
--seed--
--seed-contents--
function crossHatchedTriangles() {
return true;
}
crossHatchedTriangles();
--solutions--
// solution required