1.6 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f48d1000cf542c50ffa0 | Problema 289: Ciclos eulerianos | 5 | 301940 | problem-289-eulerian-cycles |
--description--
Considere C(x,y) como um círculo passando pelos pontos (x, y), (x, y + 1), (x + 1, y) e (x + 1, y + 1).
Para os números positivos inteiros m e n, considere E(m,n) como a configuração que consiste em m·n círculos: { C(x,y): 0 ≤ x < m, 0 ≤ y < n, sendo que x e y são números inteiros }
Um ciclo euleriano em E(m,n) é um caminho fechado que passa por cada arco exatamente uma vez. Muitos caminhos são possíveis em E(m,n), mas apenas nos interessamos por aqueles que não são cruzam a si mesmos: um caminho que não cruze a si mesmo apenas toca nos pontos da rede, mas nunca cruza a si mesmo.
A imagem abaixo mostra E(3,3) e um exemplo de um caminho que euleriano sem cruzamentos.
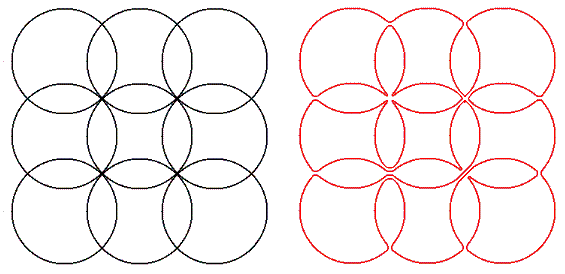
Considere L(m,n) como o número de caminhos eulerianos sem cruzamento em E(m,n). Por exemplo, L(1,2) = 2, L(2,2) = 37 e L(3,3) = 104290.
Encontre L(6,10)\bmod {10}^{10}.
--hints--
eulerianCycles() deve retornar 6567944538.
assert.strictEqual(eulerianCycles(), 6567944538);
--seed--
--seed-contents--
function eulerianCycles() {
return true;
}
eulerianCycles();
--solutions--
// solution required