2.1 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4be1000cf542c50ffd1 | Problema 338: Corte de papel de grade retangular | 5 | 301996 | problem-338-cutting-rectangular-grid-paper |
--description--
Você recebe uma folha retangular de papel de grade com dimensões em números inteiros w × h. O espaçamento da grade é de 1.
Quando cortamos as folhas ao longo das linhas da grade em duas partes e reorganizamos essas peças sem sobreposição, podemos criar novos retângulos com dimensões diferentes.
Por exemplo, a partir de uma folha com dimensões 9 × 4, podemos fazer retângulos com dimensões 18 × 2, 12 × 3 e 6 × 6 cortando e reorganizando como vemos abaixo:
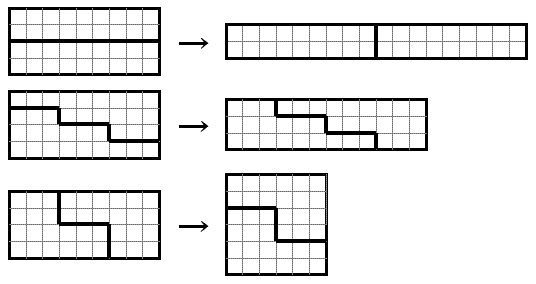
Da mesma forma, a partir de uma folha com dimensões 9 × 8, podemos fazer retângulos com dimensões 18 × 4 e 12 × 6.
Para um par w e h, considere F(w, h) como o número de retângulos distintos que podem ser feitos a partir de uma folha com dimensões w × h. Por exemplo, F(2, 1) = 0, F(2, 2) = 1, F(9, 4) = 3 e F(9, 8) = 2. Observe que os retângulos congruentes com o inicial não são contados em F(w, h). Observe também que os retângulos com dimensões w × h e as dimensões h × w não são considerados distintos.
Para um número inteiro N, considere G(N) como a soma de F(w, h) para todos os pares w e h que satisfazem 0 < h ≤ w ≤ N. Podemos verificar que G(10) = 55, G({10}^3) = 971.745 e G({10}^5) = 9.992.617.687.
Encontre G({10}^{12}). Dê sua resposta modulo {10}^8.
--hints--
cuttingRectangularGridPaper() deve retornar 15614292.
assert.strictEqual(cuttingRectangularGridPaper(), 15614292);
--seed--
--seed-contents--
function cuttingRectangularGridPaper() {
return true;
}
cuttingRectangularGridPaper();
--solutions--
// solution required