1.9 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f53d1000cf542c510050 | Problema 465: Polígonos polares | 5 | 302140 | problem-465-polar-polygons |
--description--
O núcleo de um polígono é definido pelo conjunto de pontos a partir dos quais todo o limite do polígono é visível. Definimos um polígono polar como um polígono para o qual a origem está estritamente contida no seu núcleo.
Para este problema, um polígono pode ter vértices consecutivos colineares. No entanto, um polígono ainda não pode ter autointerseções e não pode ter uma área igual a zero.
Por exemplo, apenas o primeiro dos polígonos a seguir é um polígono polar (os núcleos do segundo, terceiro, e quarto não contêm estritamente a origem e o quinto nem sequer tem um núcleo):
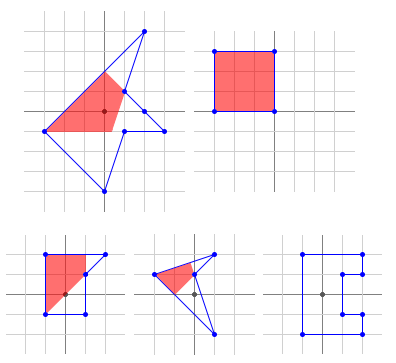
Observe que o primeiro polígono tem três vértices colineares consecutivos.
Considere P(n) como o número de polígonos polares, tal que os vértices (x, y) têm coordenadas em números inteiros, cujos valores absolutos não são maiores do que n.
Observe que os polígonos devem ser contados como diferentes se tiverem um grupo de arestas diferentes, mesmo que envolvam a mesma área. Por exemplo, o polígono com vértices [(0,0), (0,3), (1,1), (3,0)] é diferente do polígono com vértices [(0,0), (0,3), (1,1), (3,0), (1,0)].
Por exemplo, P(1) = 131, P(2) = 1.648.531, P(3) = 1.099.461.296.175 e P(343)\bmod 1.000.000.007 = 937.293.740.
Encontre P(7^{13})\bmod 1.000.000.007.
--hints--
polarPolygons() deve retornar 585965659.
assert.strictEqual(polarPolygons(), 585965659);
--seed--
--seed-contents--
function polarPolygons() {
return true;
}
polarPolygons();
--solutions--
// solution required