freeCodeCamp/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f5431000cf542c510056	Problema 471: Triângulo inscrito na elipse	5	302148	problem-471-triangle-inscribed-in-ellipse

--description--

O triângulo ΔABC está inscrito em uma elipse com equação \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, 0 < 2b < a, a e b sendo números inteiros.

Considere r(a, b) como o raio do círculo interno de ΔABC quando este tem o centro (2b, 0) e A tem coordenadas \left(\frac{a}{2}, \frac{\sqrt{3}}{2}b\right).

Por exemplo, r(3, 1) = \frac{1}{2}, r(6, 2) = 1, r(12, 3) = 2.

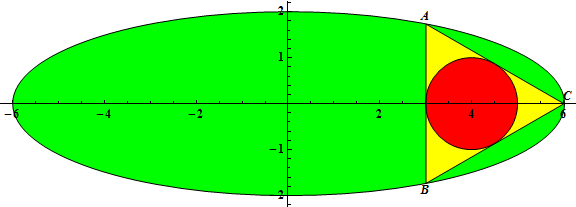
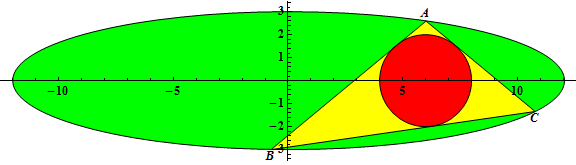
Considere G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)

Você é informado de que G(10) = 20,59722222, G(100) = 19223,60980 (arredondado para 10 dígitos significativos).

Encontre G({10}^{11}). Dê sua resposta como uma string em notação científica arredondada para 10 algarismos significativos. Use e em letra minúscula para separar a mantissa do expoente.

Para G(10), a resposta seria 2.059722222e1

--hints--

triangleInscribedInEllipse() deve retornar uma string.

assert(typeof triangleInscribedInEllipse() === 'string');

triangleInscribedInEllipse() deve retornar a string 1.895093981e31.

assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');

--seed--

--seed-contents--

function triangleInscribedInEllipse() {

  return true;
}

triangleInscribedInEllipse();

--solutions--

// solution required