freeCodeCamp/curriculum/challenges/ukrainian/10-coding-interview-prep/project-euler/problem-143-investigating-the-torricelli-point-of-a-triangle.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f3fc1000cf542c50ff0e	Завдання 143: Дослідження точок Торрічеллі	5	301772	problem-143-investigating-the-torricelli-point-of-a-triangle

--description--

Нехай ABC буде трикутником з внутрішніми кутами меншими, ніж 120 градусів. Нехай Х буде будь-якою точкою всередині трикутника, а XA = p, XC = q, і XB = r.

Ферма запропонував Торрічеллі знайти таке розміщення Х, щоб p + q + r зводилось до мінімуму.

Торрічеллі зміг довести, що якщо рівносторонні трикутники AOB, BNC та AMC будуються з кожної сторони трикутника ABC, то описані навколо AOB, BNC та AMC кола будуть перетинатися в одній точці T, всередині трикутника. Крім того, він довів, що точка Т, названа Торрічеллі / Ферма, мінімізує p + q + r. Також можна помітити, що при мінімізації суми, AN = BM = CO = p + q + r і AN, BM і CO також перетинаються в точці T.

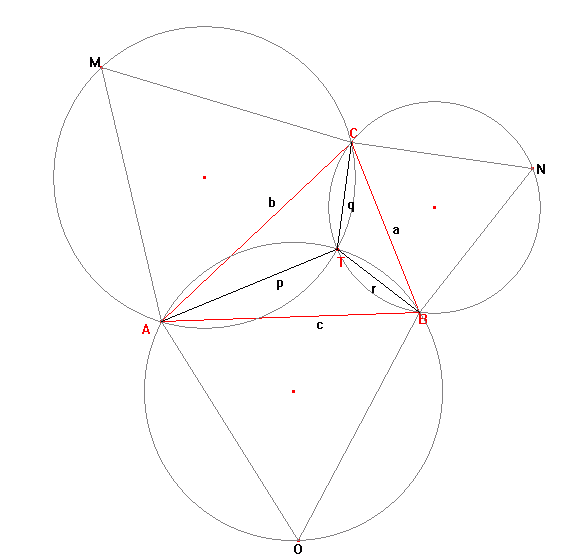
Якщо сума зведена до мінімуму і a, b, c, p, q та r - всі натуральні числа, ми будемо називати трикутник ABC трикутником Торрічеллі. Наприклад, a = 399, b = 455, c = 511 - приклад трикутника Торрічеллі з p + q + r = 784. Знайдіть суму всіх різних значень p + q + r + r ≤ 120000 для трикутників Торрічеллі.

--hints--

sumTorricelliTriangles() має повернути30758397.

assert.strictEqual(sumTorricelliTriangles(), 30758397);

--seed--

--seed-contents--

function sumTorricelliTriangles() {

  return true;
}

sumTorricelliTriangles();

--solutions--

// solution required