1.8 KiB
1.8 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f46e1000cf542c50ff80 | Завдання 257: Кутові бісектриси | 5 | 301905 | problem-257-angular-bisectors |
--description--
Дано цілочисельний трикутник ABC зі сторонами a ≤ b ≤ c. (AB = c, BC = a and AC = b).
Бісектриси кутів трикутника перетинають в точках E, F і G (див. малюнок нижче).
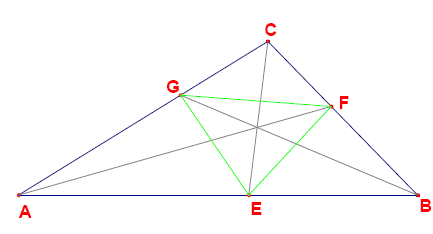
Відрізки EF, EG і FG ділять трикутник ABC на чотири менші трикутники: AEG, BFE, CGF і EFG. Можна довести, що для кожного з цих чотирьох трикутників відношення площ \frac{\text{area} (ABC)} {\text{area}\text{subtriangle})} є раціональним числом. Однак існують трикутники, у яких деякі або всі ці відношення є цілісними числами.
Скільки існує трикутників ABC з периметром ≤ 100\\,000\\,000, у яких відношення площ \frac{\text{area}(ABC)} {\text{area}(AEG)} дорівнює цілому числу?
--hints--
angularBisectors() має повернути 139012411.
assert.strictEqual(angularBisectors(), 139012411);
--seed--
--seed-contents--
function angularBisectors() {
return true;
}
angularBisectors();
--solutions--
// solution required