2.0 KiB
2.0 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4751000cf542c50ff87 | Завдання 264: Центри трикутників | 5 | 301913 | problem-264-triangle-centres |
--description--
Розглянемо всі трикутники, що мають:
- Усі їх вершини в точках решітки.
- Окружний центр у координаті О.
- Ортоцентр у точці H(5, 0).
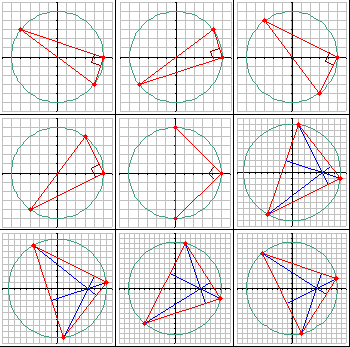
Існує дев’ять таких трикутників, які мають \text{perimeter} ≤ 50.
Перелічені та показані у порядку зростання їхнього периметра, вони:
Сума їхніх периметрів, округлена до чотирьох знаків після коми, дорівнює 291.0089.
Знайдіть усі такі трикутники з \text{perimeter} ≤ {10}^5. У відповідь введіть суму їхніх периметрів, округлену до чотирьох знаків після коми.
--hints--
triangleCentres() має повернути 2816417.1055.
assert.strictEqual(triangleCentres(), 2816417.1055);
--seed--
--seed-contents--
function triangleCentres() {
return true;
}
triangleCentres();
--solutions--
// solution required