1.9 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4761000cf542c50ff88 | Завдання 265: Двійкові кола | 5 | 301914 | problem-265-binary-circles |
--description--
2^N двійкові цифри можуть бути розміщені в колі так, що всі $N$-цифрові підпослідовності за годинниковою стрілкою відрізняються.
Для N = 3, два таких кругових розміщення можливі, ігноруючи обертання:
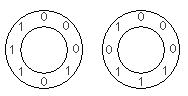
Для першого розташування, 3-значні підпослідовності за годинниковою стрілкою: 000, 001, 010, 101, 011, 111, 110 і 100.
Кожне кругове розташування може бути закодовано як число шляхом конкатенації двійкових цифр, починаючи з підпослідовності всіх нулів як найбільш значущих бітів і продовжуючи за годинниковою стрілкою. Таким чином, два варіанти розміщення для N = 3 представлені як 23 і 29:
$${00010111}_2 = 23\\ {00011101}_2 = 29$$
Називаючи S(N) сумою унікальних числових подань, ми можемо побачити, що S(3) = 23 + 29 = 52.
Знайдіть S(5).
--hints--
binaryCircles() має повернути 209110240768.
assert.strictEqual(binaryCircles(), 209110240768);
--seed--
--seed-contents--
function binaryCircles() {
return true;
}
binaryCircles();
--solutions--
// solution required