freeCodeCamp/curriculum/challenges/ukrainian/10-coding-interview-prep/project-euler/problem-275-balanced-sculptures.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f4801000cf542c50ff92	Завдання 275: Збалансовані скульптури	5	301925	problem-275-balanced-sculptures

--description--

Визначимо збалансовану скульптуру $n$-порядку наступним чином:

• Поліоміно, що складається з n + 1 плиток, відомих як блоки (n плиток) та колон (залишкові плитки);
• центр колони знаходиться в положенні (x = 0, y = 0);
• блоки мають $y$-координати, більші за нуль (тому колона - це унікальна найнижча плитка);
• центр мас разом узятих блоків, має $x$-координату, рівну нулю.

Під час підрахунку скульптур будь-які композиції, які є просто відображенням осі y, не зараховуються як окремі. Наприклад, 18 наведених нижче збалансованих скульптур 6-го порядку; зауважте, що кожна пара дзеркальних зображень (на осі y) зараховується як одна скульптура:

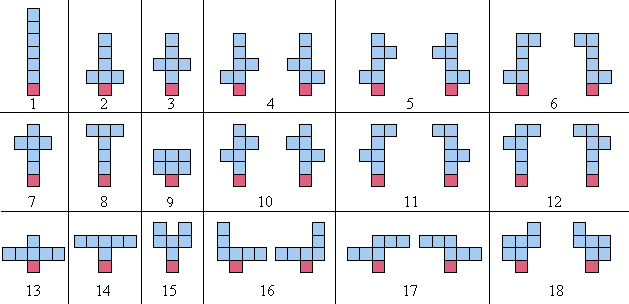
Існує 964 збалансованих скульптур 10-го порядку та 360505 15-го порядку.

Скільки тут є збалансованих скульптур 18-го порядку?

--hints--

balancedSculptures() має повернути 15030564.

assert.strictEqual(balancedSculptures(), 15030564);

--seed--

--seed-contents--

function balancedSculptures() {

  return true;
}

balancedSculptures();

--solutions--

// solution required