2.0 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f48d1000cf542c50ffa0 | Задача 289: Ейлерові ланцюги | 5 | 301940 | problem-289-eulerian-cycles |
--description--
Нехай C(x,y) – коло, що проходить через точки (x, y), (x, y + 1), (x + 1, y) та (x + 1, y + 1).
Для натуральних чисел m і n нехай E(m,n) – це конфігурація, що складається з кіл m·n: { C(x,y): 0 ≤ x < m, 0 ≤ y < n, x та y натуральні числа }
Ейлерів ланцюг на E(m,n) – це закритий шлях, який проходить через кожну дугу рівно один раз. Багато таких шляхів можливі на E(m,n), але нас цікавлять тільки ті, які не є самоперетинними: Неперетинний шлях просто торкається себе в точках ґратки, але ніколи себе не перетинає.
На зображенні нижче показано E(3,3) і наведено приклад неперетинного шляху Ейлера.
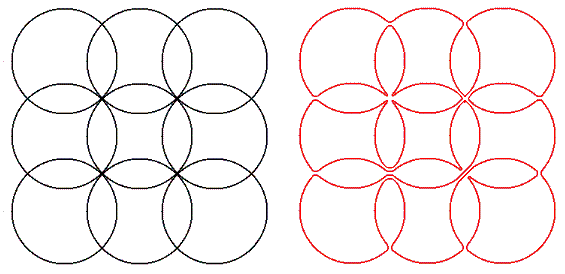
Нехай L(m,n) – кількість неперетинних шляхів Ейлера на E(m,n). Наприклад, L(1,2) = 2, L(2,2) = 37 та L(3,3) = 104290.
Знайдіть L(6,10)\bmod {10}^{10}.
--hints--
eulerianCycles() має повертати до 6567944538.
assert.strictEqual(eulerianCycles(), 6567944538);
--seed--
--seed-contents--
function eulerianCycles() {
return true;
}
eulerianCycles();
--solutions--
// solution required