2.3 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4931000cf542c50ffa6 | Завдання 295: Лінзоподібні отвори | 5 | 301947 | problem-295-lenticular-holes |
--description--
Опукла область, укладена в два кола, називається лінзоподібним отвором, якщо:
- Центри обох кіл знаходяться в точках ґратки.
- Два кола перетинаються в двох різних точках ґратки.
- Внутрішня частина опуклої області, укладеної в обидва кола, не містить ніяких точок ґратки.
Розглянемо ці кола:
$$\begin{align} & C_0: x^2 + y^2 = 25 \\ & C_1: {(x + 4)}^2 + {(y - 4)}^2 = 1 \\ & C_2: {(x - 12)}^2 + {(y - 4)}^2 = 65 \end{align}$$
Кола C_0, C_1 та C_2 намальовані на малюнку нижче.
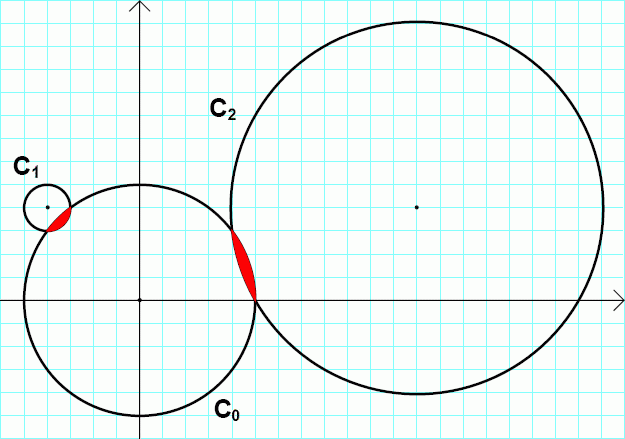
Лінзоподібний отвір утворюють як C_0 і C_1, так і C_0 і C_2.
Впорядковану пару додатних дійсних чисел (r_1, r_2) називають лінзоподібною парою, якщо існують два кола з радіусами r_1 та r_2, які утворюють лінзоподібний отвір. Можемо перевірити, що (1, 5) та (5, \sqrt{65}) – лінзоподібні пари в наведеному вище прикладі.
Припустимо, що L(N) – кількість різних лінзоподібних пар (r_1, r_2), для яких 0 < r_1 ≤ r_2 ≤ N. Можемо перевірити, що L(10) = 30 і L(100) = 3442.
Знайдіть L(100\\,000).
--hints--
lenticularHoles() має повертати до 4884650818.
assert.strictEqual(lenticularHoles(), 4884650818);
--seed--
--seed-contents--
function lenticularHoles() {
return true;
}
lenticularHoles();
--solutions--
// solution required