1.9 KiB
1.9 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5001000cf542c510012 | Завдання 404: Еліпси, що перетинаються | 5 | 302072 | problem-404-crisscross-ellipses |
--description--
E_a — еліпс з рівнянням x^2 + 4y^2 = 4a^2.
E_a' — повернуте зображення E_a на θ градусів проти годинникової стрілки навколо початку координат O(0, 0) на 0° < θ < 90°.
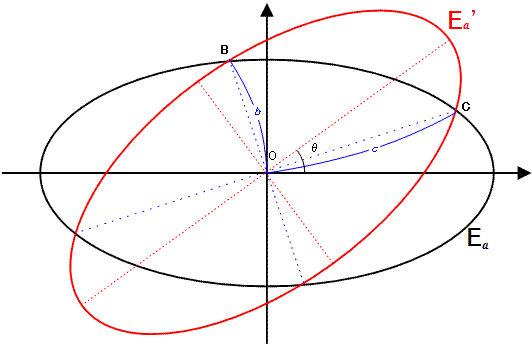
b — відстань до двох точок перетину, найближчих до початку системи координат, а c — відстань двох інших точок перетину.
Ми називаємо впорядкований триплет (a, b, c) канонічним еліпсоїдним триплетом, якщо a, b та c - додатні цілі числа.
Наприклад, (209, 247, 286) — це канонічний еліпсоїдний триплет.
Нехай C(N) — це кількість різних еліпсоїдних триплетів (a, b, c) для a ≤ N.
Можна переконатися, що C({10}^3) = 7, C({10}^4) = 106, а C({10}^6) = 11\\,845.
Знайдіть C({10}^{17}).
--hints--
crisscrossEllipses() має повернути 1199215615081353.
assert.strictEqual(crisscrossEllipses(), 1199215615081353);
--seed--
--seed-contents--
function crisscrossEllipses() {
return true;
}
crisscrossEllipses();
--solutions--
// solution required