2.2 KiB
2.2 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5131000cf542c510025 | Задача 422: Послідовність точок на гіперболі | 5 | 302092 | problem-422-sequence-of-points-on-a-hyperbola |
--description--
Нехай H - це гіпербола, визначена рівнянням 12x^2 + 7xy - 12y^2 = 625.
Визначте X як точку з координатами (7, 1). Можна побачити, що X знаходиться в H.
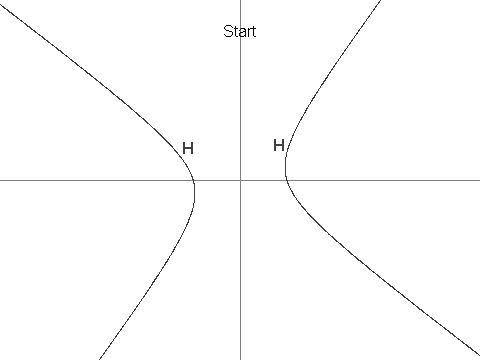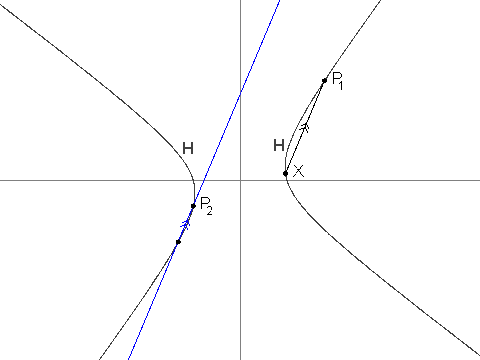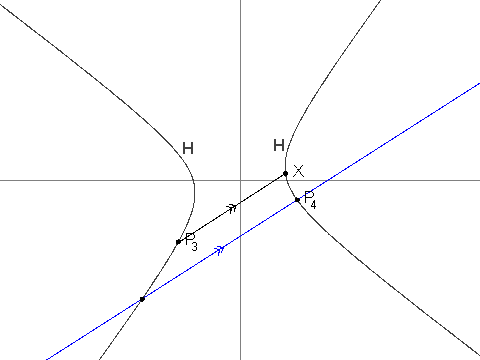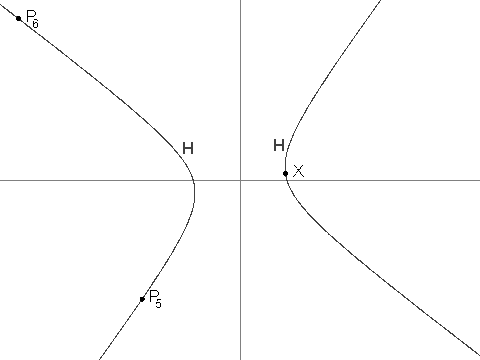
Тепер визначимо послідовність точок у H, \\{P_i : i ≥ 1\\}, як:
P_1 = (13, \frac{61}{4}).P_2 = (\frac{-43}{6}, -4).- Для
i > 2,P_iє унікальною точкою вH, яка відрізняється відP_{i - 1}. Таким чином лініяP_iP_{i - 1}паралельна до лініїP_{i - 2}X. Можна показати, щоP_iє добре визначеною і її координати завжди раціональні.
Дано, що P_3 = (\frac{-19}{2}, \frac{-229}{24}), P_4 = (\frac{1267}{144}, \frac{-37}{12}) and P_7 = (\frac{17\\,194\\,218\\,091}{143\\,327\\,232}, \frac{274\\,748\\,766\\,781}{1\\,719\\,926\\,784}).
Знайдіть P_n для n = {11}^{14} у такому форматі: Якщо P_n = (\frac{a}{b}, \frac{c}{d}), де дроби - найнижчі значення, а знаменники додатні, то відповіддю є (a + b + c + d)\bmod 1\\,000\\,000\\,007.
Для n = 7 відповідь була б такою: 806\\,236\\,837.
--hints--
sequenceOfPointsOnHyperbola() повинен повернути 92060460.
assert.strictEqual(sequenceOfPointsOnHyperbola(), 92060460);
--seed--
--seed-contents--
function sequenceOfPointsOnHyperbola() {
return true;
}
sequenceOfPointsOnHyperbola();
--solutions--
// solution required