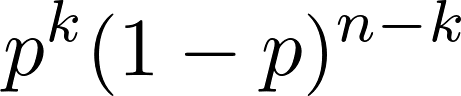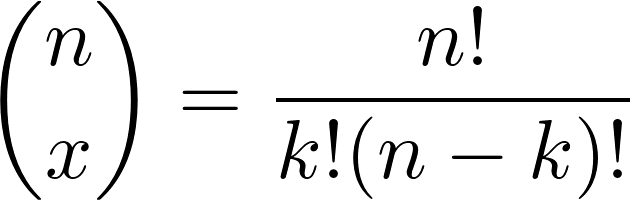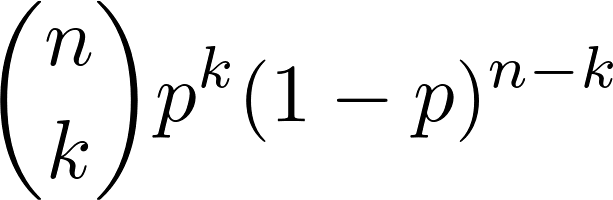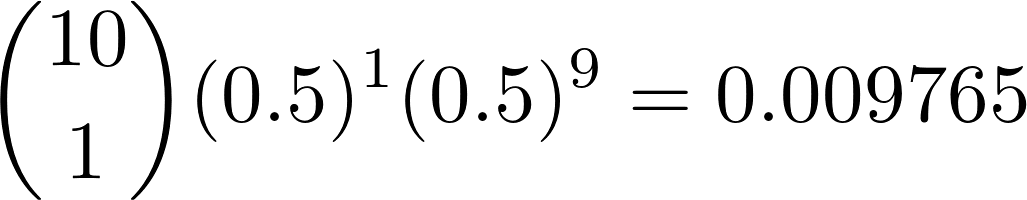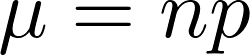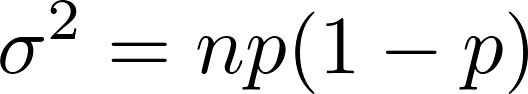freeCodeCamp/guide/russian/mathematics/statistics/binomial-distribution/index.md

title, localeTitle

title	localeTitle
Binomial Distribution	Биномиальное распределение

Биномиальное распределение

Биномиальное распределение описывает вероятность наличия ровно k успехов в n независимых испытаниях Бернулли с вероятностью успеха p .

Есть четыре условия, которые должны быть выполнены, прежде чем мы сможем использовать распределение биномалей.

1. Испытания независимы.
2. Число испытаний, n , фиксировано.
3. Каждый результат испытания можно отнести к успеху или неудаче.
4. Вероятность успеха, p , одинакова для каждого испытания.

пример

Рассмотрим эксперимент по бросанию справедливой монеты в 10 раз. Пусть результат «Головок» - это успех и результат «Хвост».

1. Бросание монеты - это одно испытание эксперимента, и каждый раз, когда мы бросаем монету, полученный результат не зависит от результата любого другого испытания.
2. Мы бросаем монету 10 раз (фиксированное значение n ).
3. Мы решили считать «Главы» успешными, а «Хвосты» - неудачей.
4. Вероятность получения голов с честной монетой равна 0,5, и это одинаково в каждом испытании.

Все четыре условия выполнены, поэтому мы можем моделировать этот эксперимент, используя биномиальное распределение.

Найдем вероятность получить Heads точно один раз, т.е. 1 успех.

Есть 10 бросков, и любой мог бы привести к исходу Heads, и каждый из этих 10 сценариев имеет ту же вероятность. Таким образом, конечная вероятность может быть записана как: [# Number of Scenarios] x P(single scenario)

Первой составляющей приведенного выше уравнения является число способов расположения k = 1 успехов среди n = 10 испытаний. Второй компонент - вероятность любого из четырех (одинаково вероятных) сценариев.

Рассмотрим P(Single Scenario) в общем случае k успехов и n - k отказов в n испытаниях. Чтобы найти значение, используйте правило умножения для независимых событий:

Количество способов получить k успехов из n проб может быть записано как n выбрать k :

Таким образом, общая формула для получения вероятности наблюдения точно k успехов в n независимых испытаниях дает:

Следовательно, вероятность получения ровно одной главы в испытаниях:

Среднее и разное

Среднее биномиальное распределение с n исследованиями, где p - вероятность успеха, определяется:

и дисперсия:

Дополнительная информация:

• OpenIntro Statistics 3rd Edition (Глава 3 - стр. 145)
• Получение среднего значения и разности биномиального распределения