* Create complex-number-plane * Change Title to complex-plane * Rename complex-plane to complex-plane.md * Rename guide/english/mathematics/complex-plane.md to guide/english/mathematics/complex-plane/index.md
1.7 KiB
title
| title |
|---|
| Complex Number Plane |
Complex Numbers
The complex number plane expresses a complex number in graphical form. The complex number is an extension of the real number line that adds an imaginary axis. This creates a two dimensional space with real and imaginary coordinates.
Complex numbers take the form (a + bi) with the real part being "a" expressed on the x-axis and "b" expressed on the y-axis. See the graph below.
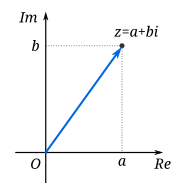
A complex number that is on the x-axis is called purely real; while a complex number that is on the y-axis only is called purely imaginary. The x-axis or real number line includes all real numbers. Therefore, the set of all real numbers is actually a subset of the complex numbers. All real numbers, then are complex numbers who imaginary component is zero.
Complex Polar Coordinates
In polar form the cooordinates are the radius to the point in the complex plane and the angle from the x-axis.
The radius[r] is found from the pythagorean formula applied to the real and imaginary componenets.
r = sqrt(a^2 + b^2)
The angle for the polar coordinate is found from taking the inverse tangent of the real and imaginary coordinates.
@ = arctan(b/a) where x > 0 @ = arctan(b/a) + pi where x < 0 @ is undefined when x = 0
