* feat(tools): add seed/solution restore script * chore(curriculum): remove empty sections' markers * chore(curriculum): add seed + solution to Chinese * chore: remove old formatter * fix: update getChallenges parse translated challenges separately, without reference to the source * chore(curriculum): add dashedName to English * chore(curriculum): add dashedName to Chinese * refactor: remove unused challenge property 'name' * fix: relax dashedName requirement * fix: stray tag Remove stray `pre` tag from challenge file. Signed-off-by: nhcarrigan <nhcarrigan@gmail.com> Co-authored-by: nhcarrigan <nhcarrigan@gmail.com>
1.8 KiB
1.8 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f3c71000cf542c50feda | Problem 91: Right triangles with integer coordinates | 5 | 302208 | problem-91-right-triangles-with-integer-coordinates |
--description--
The points P (x1, y1) and Q (x2, y2) are plotted at integer co-ordinates and are joined to the origin, O(0,0), to form ΔOPQ.
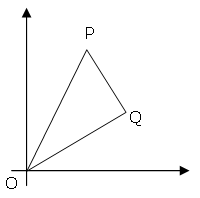
There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate lies between 0 and 2 inclusive; that is, 0 ≤ x1, y1, x2, y2 ≤ 2.
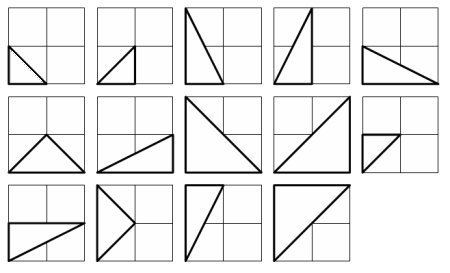
Given that 0 ≤ x1, y1, x2, y2 ≤ 50, how many right triangles can be formed?
--hints--
rightTrianglesIntCoords() should return a number.
assert(typeof rightTrianglesIntCoords() === 'number');
rightTrianglesIntCoords() should return 14234.
assert.strictEqual(rightTrianglesIntCoords(), 14234);
--seed--
--seed-contents--
function rightTrianglesIntCoords() {
return true;
}
rightTrianglesIntCoords();
--solutions--
// solution required