1.4 KiB
1.4 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4641000cf542c50ff76 | Problema 247: Quadrados sob uma hipérbole | 5 | 301894 | problem-247-squares-under-a-hyperbola |
--description--
Considere a região restringida por 1 ≤ x e 0 ≤ y ≤ \frac{1}{x}.
Considere S_1 como o maior quadrado que pode caber sob a curva.
Considere S_2 como o maior quadrado que cabe na área restante, e assim por diante.
Considere o índice de S_n como o par (esquerda, abaixo) indicando o número de quadrados à esquerda de S_n e o número de quadrados abaixo de S_n.
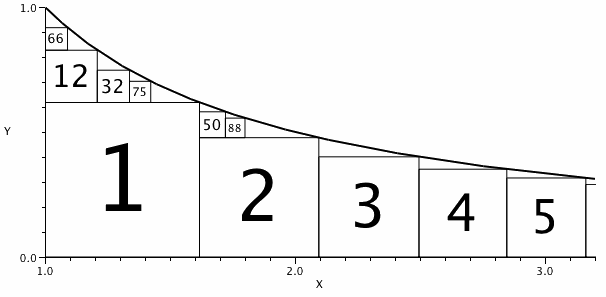
O diagrama mostra alguns desses quadrados rotulados por número.
S_2 tem um quadrado à sua esquerda e nenhum abaixo, então o índice de S_2 é (1, 0).
Podemos ver que o índice de S_{32} é (1,1) como é o índice de S_{50}.
50 é o maior n para o qual o índice de S_n é (1, 1).
3 é o maior n para o qual o índice de S_n é (3, 3)?
--hints--
squaresUnderAHyperbola() deve retornar 782252.
assert.strictEqual(squaresUnderAHyperbola(), 782252);
--seed--
--seed-contents--
function squaresUnderAHyperbola() {
return true;
}
squaresUnderAHyperbola();
--solutions--
// solution required