16 KiB
16 KiB
id, title, challengeType, forumTopicId, localeTitle
| id | title | challengeType | forumTopicId | localeTitle |
|---|---|---|---|---|
| 587d8256367417b2b2512c7a | Find the Minimum and Maximum Value in a Binary Search Tree | 1 | 301642 | Найти минимальное и максимальное значение в двоичном дереве поиска |
Description
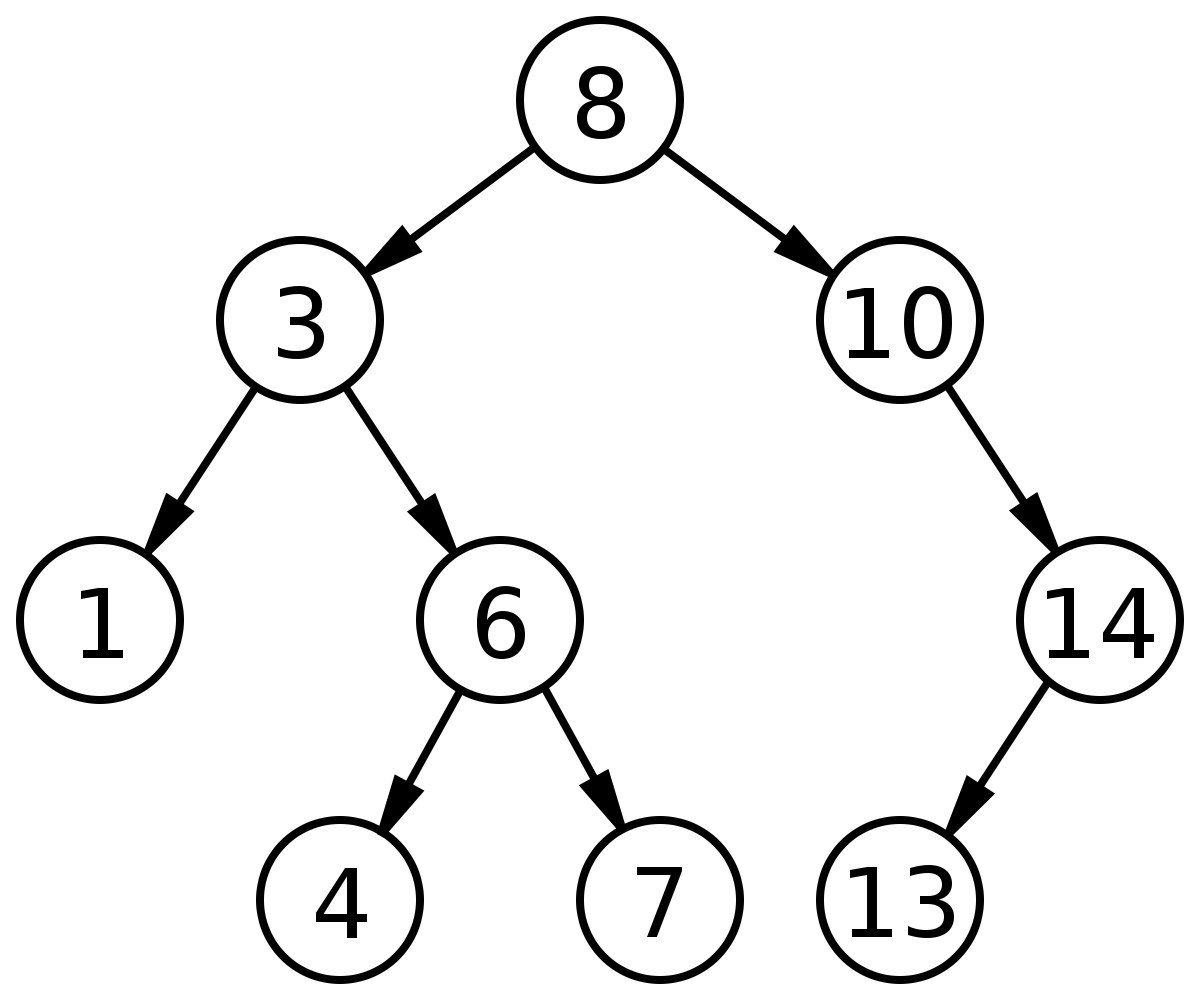
findMin и findMax . Эти методы должны возвращать минимальное и максимальное значение, хранящиеся в двоичном дереве поиска (не беспокойтесь о добавлении значений в дерево на данный момент, мы добавили некоторые в фоновом режиме). Если вы застряли, подумайте об инварианте, который должен быть истинным для двоичных деревьев поиска: каждое левое поддерево меньше или равно его родительскому элементу, и каждое правое поддерево больше или равно его родительскому. Давайте также скажем, что наше дерево может хранить только целочисленные значения. Если дерево пустое, любой метод должен возвращать значение null .
Instructions
findMin and findMax. These methods should return the minimum and maximum value held in the binary search tree (don't worry about adding values to the tree for now, we have added some in the background). If you get stuck, reflect on the invariant that must be true for binary search trees: each left subtree is less than or equal to its parent and each right subtree is greater than or equal to its parent. Let's also say that our tree can only store integer values. If the tree is empty, either method should return null.
Tests
tests:
- text: The <code>BinarySearchTree</code> data structure exists.
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() }; return (typeof test == 'object')})());
- text: The binary search tree has a method called <code>findMin</code>.
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; return (typeof test.findMin == 'function')})());
- text: The binary search tree has a method called <code>findMax</code>.
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; return (typeof test.findMax == 'function')})());
- text: The <code>findMin</code> method returns the minimum value in the binary search tree.
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; if (typeof test.findMin !== 'function') { return false; }; test.add(4); test.add(1); test.add(7); test.add(87); test.add(34); test.add(45); test.add(73); test.add(8); return test.findMin() == 1; })());
- text: The <code>findMax</code> method returns the maximum value in the binary search tree.
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; if (typeof test.findMax !== 'function') { return false; }; test.add(4); test.add(1); test.add(7); test.add(87); test.add(34); test.add(45); test.add(73); test.add(8); return test.findMax() == 87; })());
- text: The <code>findMin</code> and <code>findMax</code> methods return <code>null</code> for an empty tree.
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; if (typeof test.findMin !== 'function') { return false; }; if (typeof test.findMax !== 'function') { return false; }; return (test.findMin() == null && test.findMax() == null) })());
Challenge Seed
var displayTree = tree => console.log(JSON.stringify(tree, null, 2));
function Node(value) {
this.value = value;
this.left = null;
this.right = null;
}
function BinarySearchTree() {
this.root = null;
// change code below this line
// change code above this line
}
After Tests
BinarySearchTree.prototype = {
add: function(value) {
var node = this.root;
if (node == null) {
this.root = new Node(value);
return;
} else {
function searchTree(node) {
if (value < node.value) {
if (node.left == null) {
node.left = new Node(value);
return;
} else if (node.left != null) {
return searchTree(node.left);
}
} else if (value > node.value) {
if (node.right == null) {
node.right = new Node(value);
return;
} else if (node.right != null) {
return searchTree(node.right);
}
} else {
return null;
}
}
return searchTree(node);
}
}
};
Solution
var displayTree = tree => console.log(JSON.stringify(tree, null, 2));
function Node(value) {
this.value = value;
this.left = null;
this.right = null;
}
function BinarySearchTree() {
this.root = null;
this.findMin = function() {
// Empty tree.
if (!this.root) {
return null;
}
let currentNode = this.root;
while (currentNode.left) {
currentNode = currentNode.left;
}
return currentNode.value;
};
this.findMax = function() {
// Empty tree.
if (!this.root) {
return null;
}
let currentNode = this.root;
while (currentNode.right) {
currentNode = currentNode.right;
}
return currentNode.value;
};
this.add = function(value) {
// Empty tree.
if (!this.root) {
this.root = new Node(value);
return undefined;
}
return this.addNode(this.root, value);
};
this.addNode = function(node, value) {
// Check if value already exists.
if (node.value === value) return null;
if (value < node.value) {
if (node.left) {
return this.addNode(node.left, value);
} else {
node.left = new Node(value);
return undefined;
}
} else {
if (node.right) {
return this.addNode(node.right, value);
} else {
node.right = new Node(value);
return undefined;
}
}
};
this.isPresent = function(value) {
if (!this.root) {
return null;
}
return this.isNodePresent(this.root, value);
};
this.isNodePresent = function(node, value) {
if (node.value === value) return true;
if (value < node.value) {
return node.left ? this.isNodePresent(node.left, value) : false;
} else {
return node.right ? this.isNodePresent(node.right, value) : false;
}
return false;
};
this.findMinHeight = function() {
if (!this.root) {
return -1;
}
let heights = {};
let height = 0;
this.traverseTree(this.root, height, heights);
return Math.min(...Object.keys(heights));
};
this.findMaxHeight = function() {
if (!this.root) {
return -1;
}
let heights = {};
let height = 0;
this.traverseTree(this.root, height, heights);
return Math.max(...Object.keys(heights));
};
this.traverseTree = function(node, height, heights) {
if (node.left === null && node.right === null) {
return (heights[height] = true);
}
if (node.left) {
this.traverseTree(node.left, height + 1, heights);
}
if (node.right) {
this.traverseTree(node.right, height + 1, heights);
}
};
this.isBalanced = function() {
return this.findMaxHeight() > this.findMinHeight() + 1;
};
// DFS tree traversal.
this.inorder = function() {
if (!this.root) return null;
let result = [];
function traverseInOrder(node) {
if (node.left) traverseInOrder(node.left);
result.push(node.value);
if (node.right) traverseInOrder(node.right);
}
traverseInOrder(this.root);
return result;
};
this.preorder = function() {
if (!this.root) return null;
let result = [];
function traverseInOrder(node) {
result.push(node.value);
if (node.left) traverseInOrder(node.left);
if (node.right) traverseInOrder(node.right);
}
traverseInOrder(this.root);
return result;
};
this.postorder = function() {
if (!this.root) return null;
let result = [];
function traverseInOrder(node) {
if (node.left) traverseInOrder(node.left);
if (node.right) traverseInOrder(node.right);
result.push(node.value);
}
traverseInOrder(this.root);
return result;
};
// BFS tree traversal.
this.levelOrder = function() {
if (!this.root) return null;
let queue = [this.root];
let result = [];
while (queue.length) {
let node = queue.shift();
result.push(node.value);
if (node.left) queue.push(node.left);
if (node.right) queue.push(node.right);
}
return result;
};
this.reverseLevelOrder = function() {
if (!this.root) return null;
let queue = [this.root];
let result = [];
while (queue.length) {
let node = queue.shift();
result.push(node.value);
if (node.right) queue.push(node.right);
if (node.left) queue.push(node.left);
}
return result;
};
// Delete a leaf node.
}
let bst = new BinarySearchTree();