1.8 KiB
1.8 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f3ec1000cf542c50feff | 問題 128: 六角形タイルの差 | 5 | 301755 | problem-128-hexagonal-tile-differences |
--description--
1 番の六角形タイルは、12 時の位置から反時計回りに配置された 2 番から 7 番の 6 枚の六角形タイルの輪に囲まれています。
同様に、8 番から 19 番、20 番から 37 番、38 番から 61 番、… という具合に新しい輪が追加されていきます。 下図は、最初の 3 個の輪を示しています。
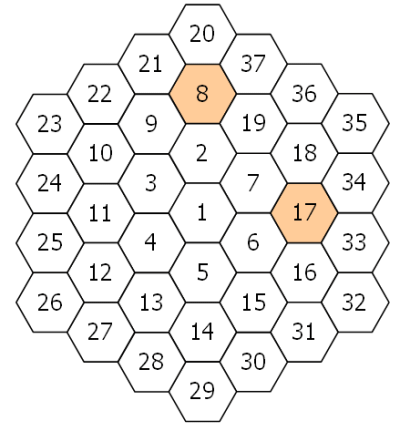
タイル n 番と、それに隣接する 6 枚の各タイルとの差を求め、差が素数となるタイルの枚数を $PD(n) とします。
例えば、タイル 8 番の周りを時計回りに差を求めると、12, 29, 11, 6, 1, 13 となります。 したがって、PD(8) = 3 です。
同様に、タイル 17 番とその周囲との差は 1, 17, 16, 1, 11, 10 なので、PD(17) = 2 です。
PD(n) の最大値が 3 であることを示すことができます。
PD(n) = 3 が成り立つすべてのタイルを昇順に並べて数列を作ると、第 10 項はタイル 271 番です。
この数列の 第 2000 項のタイルの番号を求めなさい。
--hints--
hexagonalTile() は 14516824220 を返す必要があります。
assert.strictEqual(hexagonalTile(), 14516824220);
--seed--
--seed-contents--
function hexagonalTile() {
return true;
}
hexagonalTile();
--solutions--
// solution required