1.5 KiB
1.5 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4761000cf542c50ff88 | 問題 265: 2 進数の円 | 5 | 301914 | problem-265-binary-circles |
--description--
2 進数の数字 2^N 個を、時計回りの N 桁の部分列がすべて相異なるように円形に並べることができます。
$N = 3$のとき、回転を無視すればこのような円形の配置は 2 通りあります。
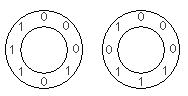
1 つ目の配置では、3 桁の部分列は時計回りに 000, 001, 010, 101, 011, 111, 110, 100 です。
0 のみからなる部分列を最上位の数字としてそこから開始し、時計回りに 2 進法の数字をつなげていくと、それぞれの円形配置を 1 つの数に変換できます。 したがって、N = 3 のとき、上の 2 つの配置は次のように 23 および 29 として表されます。
$${00010111}_2 = 23\\ {00011101}_2 = 29$$
一意の数値表現の和を S(N) とすると、S(3) = 23 + 29 = 52 であることが分かります。
S(5) を求めなさい。
--hints--
binaryCircles() は 209110240768 を返す必要があります。
assert.strictEqual(binaryCircles(), 209110240768);
--seed--
--seed-contents--
function binaryCircles() {
return true;
}
binaryCircles();
--solutions--
// solution required