freeCodeCamp/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-281-pizza-toppings.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f4861000cf542c50ff98	Problem 281: Pizza Toppings	5	301932	problem-281-pizza-toppings

--description--

You are given a pizza (perfect circle) that has been cut into m·n equal pieces and you want to have exactly one topping on each slice.

Let f(m,n) denote the number of ways you can have toppings on the pizza with m different toppings (m ≥ 2), using each topping on exactly n slices (n ≥ 1). Reflections are considered distinct, rotations are not.

Thus, for instance, f(2,1) = 1, f(2,2) = f(3,1) = 2 and f(3,2) = 16. f(3,2) is shown below:

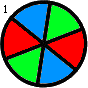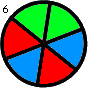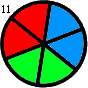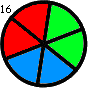
Find the sum of all f(m,n) such that f(m,n) ≤ {10}^{15}.

--hints--

pizzaToppings() should return 1485776387445623.

assert.strictEqual(pizzaToppings(), 1485776387445623);

--seed--

--seed-contents--

function pizzaToppings() {

  return true;
}

pizzaToppings();

--solutions--

// solution required