1.4 KiB
1.4 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4641000cf542c50ff76 | Problema 247: Quadrati sotto un'iperbole | 5 | 301894 | problem-247-squares-under-a-hyperbola |
--description--
Considera la regione delimitata da 1 ≤ x e 0 ≤ y ≤ \frac{1}{x}.
Sia S_1 il quadrato più grande che può stare sotto la curva.
Sia S_2 il quadrato più grande che si adatta all'area rimanente, e così via.
Sia l'indice di S_n la coppia (sinistra, sotto) indicante il numero di quadrati a sinistra di S_n e il numero di quadrati sotto S_n.
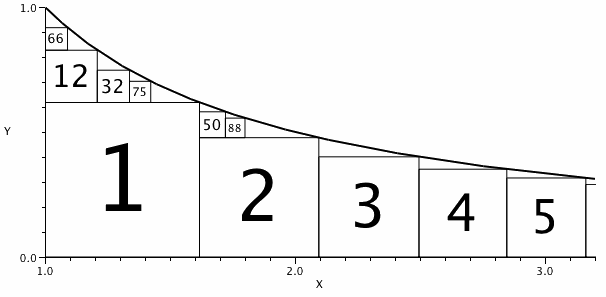
Il diagramma mostra alcuni di questi quadrati etichettati per numero.
S_2 ha un quadrato alla sua sinistra e nessuno sotto, quindi l'indice di S_2 è (1, 0).
Si può vedere che l'indice di S_{32} è (1,1) perché è l'indice di S_{50}.
50 è il più grande n per il quale l'indice di S_n è (1, 1).
Qual è il più grande n per il quale l'indice di S_n è (3, 3)?
--hints--
squaresUnderAHyperbola() dovrebbe restituire 782252.
assert.strictEqual(squaresUnderAHyperbola(), 782252);
--seed--
--seed-contents--
function squaresUnderAHyperbola() {
return true;
}
squaresUnderAHyperbola();
--solutions--
// solution required