freeCodeCamp/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f4ba1000cf542c50ffcd	Problema 334: Versare i fagioli	5	301992	problem-334-spilling-the-beans

--description--

Nel paradiso di Platone, esiste un numero infinito di ciotole in linea retta. Ogni ciotola contiene alcuni o nessuno di un numero finito di fagioli. Un bambino gioca un gioco, che permette un solo tipo di mossa: rimuovere due fagioli da qualsiasi ciotola, e metterne uno in ognuna delle due ciotole adiacenti. Il gioco termina quando ogni ciotola contiene uno o nessun fagiolo.

Ad esempio, considera due ciotole adiacenti contenenti 2 e 3 fagioli rispettivamente, tutte le altre ciotole sono vuote. Le seguenti otto mosse finiranno il gioco:

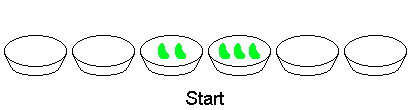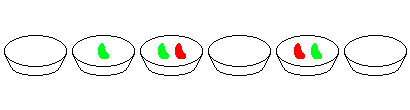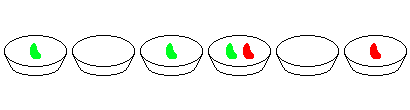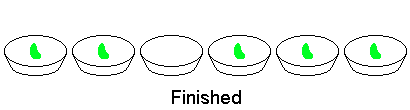
animazione di una partita con due ciotole adiacenti contenenti rispettivamente 2 e 3 fagioli:

$$\begin{align} & t_0 = 123456, \\ & t_i = \begin{cases} \frac{t_{i - 1}}{2}, & \text{if t_{i - 1} is even} \\ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{if t_{i - 1} is odd} \end{cases} \\ & \qquad \text{dove$⌊x⌋$ è la funzione arrotonda verso il basso e \oplus è l'operatore bitwise XOR.} \\ & b_i = (t_i\bmod 2^{11}) + 1. \end{align}$$

I primi due termini dell'ultima sequenza sono b_1 = 289 e b_2 = 145. Se iniziamo con b_1 e b_2 fagioli in due ciotole adiacenti, saranno necessarie 3419100 mosse per finire la partita.

Considera ora 1500 ciotole adiacenti contenenti rispettivamente b_1, b_2, \ldots, b_{1500} fagioli, tutte le altre ciotole sono vuote. Trova quante mosse sono necessarie prima che il gioco finisca.

--hints--

spillingTheBeans() dovrebbe restituire 150320021261690850.

assert.strictEqual(spillingTheBeans(), 150320021261690850);

--seed--

--seed-contents--

function spillingTheBeans() {

  return true;
}

spillingTheBeans();

--solutions--

// solution required