Files

camperbot 3d3972f2dd chore(i18n,learn): processed translations (#45333 )

2022-03-04 19:46:29 +05:30

1.4 KiB

Raw Permalink Blame History

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f5081000cf542c510019	Problema 411: Percorsi in salita	5	302080	problem-411-uphill-paths

--description--

Sia n un numero intero positivo. Supponiamo che ci siano delle stazioni alle coordinate (x, y) = (2^i\bmod n, 3^i\bmod n) per 0 ≤ i ≤ 2n. Considereremo le stazioni con le stesse coordinate come una stessa stazione.

Vogliamo formare un percorso da (0, 0) a (n, n) in modo che le coordinate x e y non diminuiscano mai.

Sia S(n) il numero massimo di stazioni che un percorso può attraversare.

Ad esempio, se n = 22, ci sono 11 stazioni distinte, e un percorso valido può passare attraverso al massimo 5 stazioni. Pertanto, S(22) = 5. Il caso è illustrato di seguito, con un esempio di percorso ottimale:

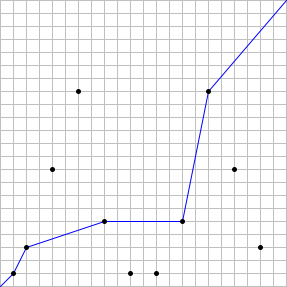
percorso valido che attraversa 5 stazioni, per n = 22, con 11 stazioni distinte

Può anche essere verificato che S(123) = 14 e S(10\\,000) = 48.

Trova \sum S(k^5) per 1 ≤ k ≤ 30.

--hints--

uphillPaths() dovrebbe restituire 9936352.

assert.strictEqual(uphillPaths(), 9936352);

--seed--

--seed-contents--

function uphillPaths() {

  return true;
}

uphillPaths();

--solutions--

// solution required

1.4 KiB Raw Permalink Blame History