1.8 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4691000cf542c50ff7b | Problema 252: Orifícios convexos | 5 | 301900 | problem-252-convex-holes |
--description--
Dado um conjunto de pontos em um plano, definimos um orifício convexo como um polígono convexo que tenha como vértices qualquer um dos pontos dados e não contenha nenhum dos pontos dados em seu interior (além dos vértices, outros pontos dados podem estar no perímetro do polígono).
Como exemplo, a imagem abaixo apresenta um conjunto de vinte pontos e alguns desses orifícios convexos. O orifício convexo mostrado como um heptágono vermelho tem uma área igual a 1049694,5 unidades quadradas, que é a maior área possível para um orifício convexo no conjunto de pontos fornecido.
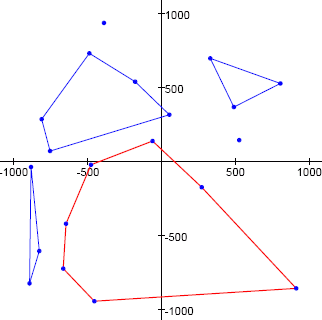
Para nosso exemplo, usamos os primeiros 20 pontos (T_{2k − 1}, T_{2k}), para k = 1, 2, \ldots, 20, produzido com o gerador de números pseudoaleatório:
$$\begin{align} S_0 & = 290.797 \\ S_{n+1} & = {S_n}^2 \; \text{mod} \; 50.515.093 \\ T_n & = (S_n \; \text{mod} \; 2000) − 1000 \end{align}$$
por exemplo: (527, 144), (-488, 732), (-454, − 947), …
Qual é a área máxima para um orifício convexo no conjunto que contém os primeiros 500 pontos da sequência pseudoaleatória? Dê sua resposta com 1 algarismo após o ponto (1 casa depois da vírgula).
--hints--
convexHoles() deve retornar 104924.
assert.strictEqual(convexHoles(), 104924);
--seed--
--seed-contents--
function convexHoles() {
return true;
}
convexHoles();
--solutions--
// solution required