1.9 KiB
1.9 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f49f1000cf542c50ffb1 | Problema 306: Jogo das tiras de papel | 5 | 301960 | problem-306-paper-strip-game |
--description--
O jogo a seguir é um exemplo clássico da Teoria Combinatória de Jogos:
Dois jogadores começam com uma tira de papel com n quadrados brancos e eles revezam turnos. Em cada turno, um jogador escolhe dois quadrados brancos vizinhos e os pinta de preto. O primeiro jogador que não puder fazer um movimento perde.
n = 1: Sem movimentos válidos, então o primeiro jogador perde automaticamente.n = 2: Apenas um movimento válido, após o qual o segundo jogador perde.n = 3: Dois movimentos válidos, mas ambos deixam uma situação na qual o segundo jogador perde.n = 4: Há três movimentos válidos para o primeiro jogador; ele é capaz de vencer o jogo pintando os dois quadrados do meio.n = 5: Quatro movimentos válidos para o primeiro jogador (mostrado abaixo em vermelho); mas não importa o que o jogador faça, o segundo jogador (azul) ganha.
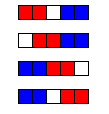
Então, para 1 ≤ n ≤ 5, há 3 valores de n para os quais o primeiro jogador pode forçar uma vitória.
Da mesma forma, para 1 ≤ n ≤ 50, há 40 valores de n para os quais o primeiro jogador pode forçar uma vitória.
Para 1 ≤ n ≤ 1.000.000, quantos valores de n existem para os quais o primeiro jogador pode forçar uma vitória?
--hints--
paperStripGame() deve retornar 852938.
assert.strictEqual(paperStripGame(), 852938);
--seed--
--seed-contents--
function paperStripGame() {
return true;
}
paperStripGame();
--solutions--
// solution required