1.9 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4b71000cf542c50ffca | Problema 331: Viradas cruzadas | 5 | 301989 | problem-331-cross-flips |
--description--
Discos NxN são colocados em um tabuleiro de jogo quadrado. Cada disco tem um lado preto e um lado branco.
A cada turno você pode escolher um disco e virar todos os discos na mesma linha e na mesma coluna que este disco: portanto, 2 × N - 1 discos são virados. O jogo termina quando todos os discos mostrarem o lado branco. O exemplo a seguir mostra um jogo em um tabuleiro 5×5.
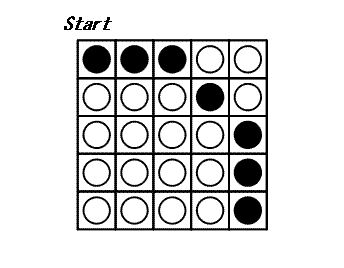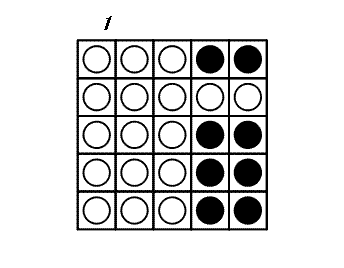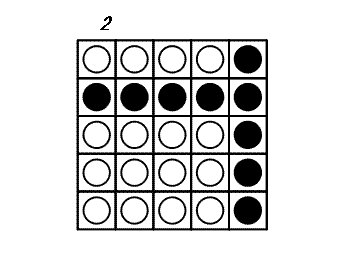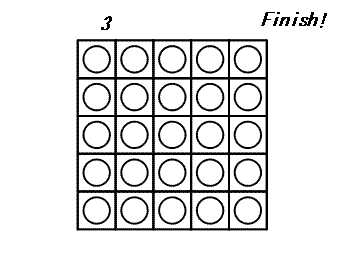
Pode-se provar que 3 é o número mínimo de turnos para terminar este jogo.
O disco do canto inferior esquerdo no tabuleiro N×N tem coordenadas (0, 0). O disco inferior direito tem coordenadas (N - 1,$0$) e o disco superior esquerdo têm coordenadas (0,$N - 1$).
Considere C_N como sendo a seguinte configuração de tabuleiro com N × N discos: um disco em (x, y) satisfazendo N - 1 \le \sqrt{x^2 + y^2} \lt N, shows exibe o lado preto; do contrário, ele exibe o lado branco. C_5 é mostrado acima.
Considere T(N) como o número mínimo de turnos para concluir um jogo começando da configuração C_N ou 0 se a configuração C_N não tiver resolução. Mostramos que T(5) = 3. Você também é informado de que T(10) = 29 e T(1.000) = 395.253.
Encontre \displaystyle \sum_{i = 3}^{31} T(2^i - i).
--hints--
crossFlips() deve retornar 467178235146843500.
assert.strictEqual(crossFlips(), 467178235146843500);
--seed--
--seed-contents--
function crossFlips() {
return true;
}
crossFlips();
--solutions--
// solution required