1.8 KiB
1.8 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5131000cf542c510025 | Problema 422: Sequência de pontos em uma hipérbole | 5 | 302092 | problem-422-sequence-of-points-on-a-hyperbola |
--description--
Considere H como a hipérbole definida pela equação 12x^2 + 7xy - 12y^2 = 625.
Em seguida, defina X como o ponto (7, 1). Pode-se ver que X está em H.
Definiremos uma sequência de pontos em H, \\{P_i : i ≥ 1\\}, como:
P_1 = (13, \frac{61}{4}).P_2 = (\frac{-43}{6}, -4).- Para
i > 2,P_ié o único pontoHque é diferente deP_{i - 1}e tal que a linhaP_iP_{i - 1}é paralela à linhaP_{i - 2}X. Pode-se ver queP_iestá corretamente definido e que suas coordenadas são sempre racionais.
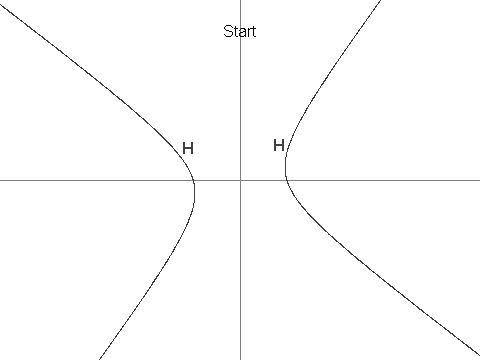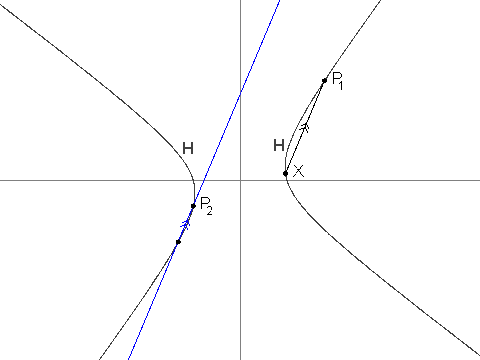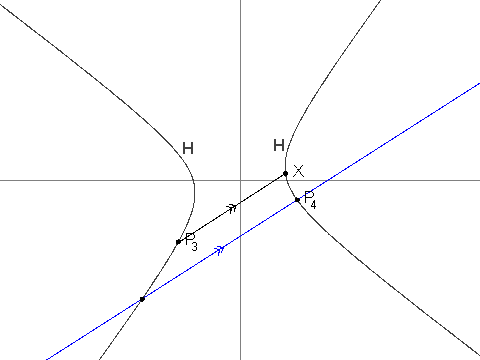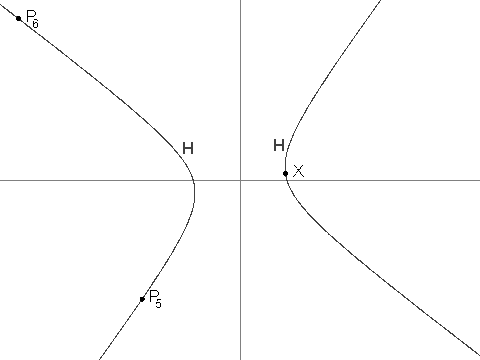
Você é informado de que P_3 = (\frac{-19}{2}, \frac{-229}{24}), P_4 = (\frac{1267}{144}, \frac{-37}{12}) and P_7 = (\frac{17.194.218.091}{143.327.232}, \frac{274.748.766.781}{1.719.926.784}).
Encontre P_n para n = {11}^{14} no seguinte formato: se P_n = (\frac{a}{b}, \frac{c}{d}), onde as frações estão nos menores termos e os denominadores são positivos, então a resposta é (a + b + c + d)\bmod 1.000.000.007.
Para n = 7, a resposta seria: 806.236.837.
--hints--
sequenceOfPointsOnHyperbola() deve retornar 92060460.
assert.strictEqual(sequenceOfPointsOnHyperbola(), 92060460);
--seed--
--seed-contents--
function sequenceOfPointsOnHyperbola() {
return true;
}
sequenceOfPointsOnHyperbola();
--solutions--
// solution required