2.6 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f53d1000cf542c510050 | Завдання 465: Полярні багатокутники | 5 | 302140 | problem-465-polar-polygons |
--description--
Ядро багатокутника визначається сукупністю точок, з яких видно сторони багатокутника. Ми визначаємо полярний багатокутник як багатокутник, джерело якого міститься суворо всередині ядра.
У такому випадку багатокутник може мати послідовні колінеарні вершини. Однак він не може перетинатися та мати нульову площу.
Наприклад, тільки перший з наведених багатокутників є полярним (ядра другого, третього та четвертого не вміщують джерело повністю, а п'ятий взагалі не має ядра):
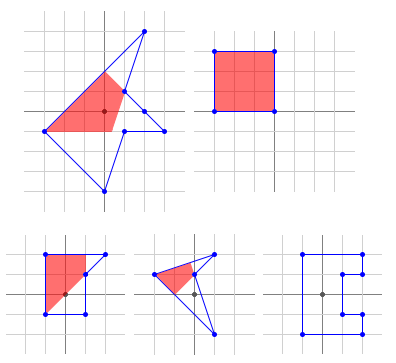
Зверніть увагу, що перший багатокутник має три послідовні колінеарні вершини.
Нехай P(n) буде кількістю полярних багатокутників, вершини яких (x, y) мають цілі координати, абсолютні значення яких не більші за n.
Зверніть увагу, що багатокутники вважаються різними, якщо вони мають різний набір сторін, навіть якщо вони оточують одну й ту ж саму область. Наприклад, багатокутник з вершинами [(0,0), (0,3), (1,1), (3,0)] відрізняється від багатокутника, що має вершини [(0,0), (0,0), (1,1), (3,0), (3,0), (1,0)].
Наприклад, P(1) = 131, P(2) = 1\\,648\\,531, P(= 1\\,099\\,461\\,296\\,175 та P(343)\bmod 1\\,000\\,007 = 937\\,293\\,740.
Знайдіть P(7^{13})\bmod 1\\,000\\,007.
--hints--
polarPolygons() повинен повертатися як 585965659.
assert.strictEqual(polarPolygons(), 585965659);
--seed--
--seed-contents--
function polarPolygons() {
return true;
}
polarPolygons();
--solutions--
// solution required